题目内容
运货卡车以每小时x千米的速度匀速行驶130千米（50≤x≤100）（单位：千米/小时）．假设汽油的价格是每升2元，而汽车每小时耗油（2+
）升，司机的工资是每小时14元．
（1）求这次行车总费用y关于x的表达式；
（2）当x为何值时，这次行车的总费用最低，并求出最低费用的值．
| x2 | 360 |
（1）求这次行车总费用y关于x的表达式；
（2）当x为何值时，这次行车的总费用最低，并求出最低费用的值．
分析：（1）求出车所用时间，根据汽油的价格是每升2元，而汽车每小时耗油（2+
）升，司机的工资是每小时14元，可得行车总费用；
（2）利用基本不等式，即可求得这次行车的总费用最低．
| x2 |
| 360 |
（2）利用基本不等式，即可求得这次行车的总费用最低．
解答：解：（1）行车所用时间为t=
(h)，
根据汽油的价格是每升2元，而汽车每小时耗油（2+
）升，司机的工资是每小时14元，可得行车总费用：
y=
×2×(2+
)+
=
+
（50≤x≤100）
（2）y=
+
≥26
，当且仅当
=
，即x=18
时，等号成立
∴当x=18
时，这次行车的总费用最低，最低费用为26
元．
| 130 |
| x |
根据汽油的价格是每升2元，而汽车每小时耗油（2+
| x2 |
| 360 |
y=
| 130 |
| x |
| x2 |
| 360 |
| 14×130 |
| x |
| 2340 |
| x |
| 13x |
| 18 |
（2）y=
| 2340 |
| x |
| 13x |
| 18 |
| 10 |
| 2340 |
| x |
| 13x |
| 18 |
| 10 |
∴当x=18
| 10 |
| 10 |
点评：本题考查函数模型的构建，考查利用基本不等式求最值，确定函数的模型是关键．
练习册系列答案
相关题目
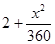）升，司机的工资是每小时14元.