题目内容
已知定义在R上的函数f(x)满足f(2-x)+f(x)=0和f(x-2)+f(x)=0,且当x∈[1,2]时f(x)=1-(x-2)2.若直线y=kx(k为常数),与函数f(x)的图象在区间(-2,5)上恰有4个公共点,则实数k的取值范围是( )
A、(2
| ||
B、(2
| ||
C、(-
| ||
D、(-
|
分析:依题意,可求得y=f(x)的图象关于(1,0)对称;①是偶函数;②是以4k(k∈Z且k≠0)为周期的函数;③函数f(x)关于直线x=2对称,④;依此作图,及可求得答案.
解答:解:∵f(2-x)+f(x)=0,
∴y=f(x)的图象关于(1,0)成中心对称对称;①
又f(x-2)+f(x)=0,
∴f(2-x)=f(x-2)=f[-(2-x)],
∴函数f(x)为偶函数;②
又f(x-2)+f(x)=0,
∴f(x-2)=-f(x),
∴f(x-4)=-f(x-2)=f(x),
∴函数f(x)是以4k(k∈Z且k≠0)为周期的函数;③
由函数f(x)为偶函数得:f(2-x)+f(x)=0?f(2+x)+f(-x)=0?f(2+x)+f(x)=0,
∴f(2+x)=f(2-x),即函数f(x)关于直线x=2对称,④
又当x∈[1,2]时f(x)=1-(x-2)2,
∴由①②③④作图如下:
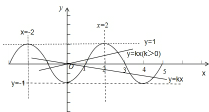
由图知,当k>0时,直线y=kx(k为常数)与函数f(x)的图象在区间(-2,5)上恰有3个公共点,不符合题意;
∴k<0,令y=g(x)=kx,
则g(4)=4k>-1,
解得:-
<k<0.
故选:D.
∴y=f(x)的图象关于(1,0)成中心对称对称;①
又f(x-2)+f(x)=0,
∴f(2-x)=f(x-2)=f[-(2-x)],
∴函数f(x)为偶函数;②
又f(x-2)+f(x)=0,
∴f(x-2)=-f(x),
∴f(x-4)=-f(x-2)=f(x),
∴函数f(x)是以4k(k∈Z且k≠0)为周期的函数;③
由函数f(x)为偶函数得:f(2-x)+f(x)=0?f(2+x)+f(-x)=0?f(2+x)+f(x)=0,
∴f(2+x)=f(2-x),即函数f(x)关于直线x=2对称,④
又当x∈[1,2]时f(x)=1-(x-2)2,
∴由①②③④作图如下:

由图知,当k>0时,直线y=kx(k为常数)与函数f(x)的图象在区间(-2,5)上恰有3个公共点,不符合题意;
∴k<0,令y=g(x)=kx,
则g(4)=4k>-1,
解得:-
| 1 |
| 4 |
故选:D.
点评:本题考查抽象函数及其应用,着重考查函数的零点与方程根的关系,考查函数的对称性、周期性、奇偶性的综合应用,考查转化思想与作图能力,属于难题.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |