题目内容
3．当x∈（0，2）时，求函数f（x）=ex-ex的值域．分析 求出原函数的导函数，得到极值点，再求出极值及端点值得答案．
解答 解：∵f（x）=ex-ex，
∴f′（x）=ex-e，
令f′（x）=0，得x=1，
∴当x∈（0，1）时，函数f（x）单调递减，当x∈（1，2）时，f（x）单调递增，
又f（0）=1，f（2）=e2-2e，f（1）=0．
∴f（x）的值域为[0，e2-2e）．
点评 本题考查交集及其运算，考查了利用导数求函数的最值，是中档题．
练习册系列答案
相关题目
13．下面不等式不成立的是（ ）
| A． | 90.7＜90.8 | B． | ${（{\frac{1}{2}}）^{-0.1}}$＞${（{\frac{1}{2}}）^{0.1}}$ | C． | log20.6＜log20.8 | D． | log0.25＞log0.22 |
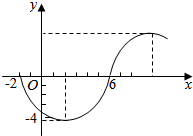函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜π）的部分图象如图所示．