题目内容
(本题满分12分)已知二次函数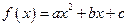 满足条件:①
满足条件:①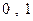 是
是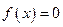 的两个零点;②
的两个零点;②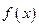 的最小值为
的最小值为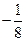
(1)求函数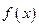 的解析式;
的解析式;
(2)设数列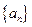 的前
的前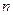 项积为
项积为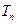 ,且
,且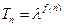 ,
,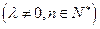 ,求数列
,求数列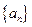 的前
的前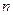 项和
项和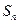
(3)在(2)的条件下,当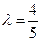 时,若
时,若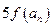 是
是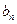 与
与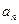 的等差中项,试问数列
的等差中项,试问数列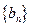 中
中
第几项的值最小?并求出这个最小值。
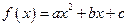 满足条件:①
满足条件:①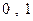 是
是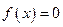 的两个零点;②
的两个零点;②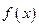 的最小值为
的最小值为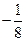
(1)求函数
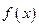 的解析式;
的解析式;(2)设数列
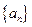 的前
的前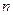 项积为
项积为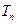 ,且
,且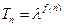 ,
,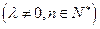 ,求数列
,求数列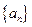 的前
的前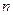 项和
项和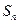
(3)在(2)的条件下,当
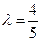 时,若
时,若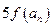 是
是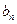 与
与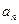 的等差中项,试问数列
的等差中项,试问数列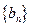 中
中第几项的值最小?并求出这个最小值。
解:(1)由题意知 :解得
:解得 ,故
,故
(2)因 ,当
,当 时,
时, ,所以
,所以 ,又
,又 ,满足上式
,满足上式 ,当
,当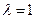 时,
时, ,当
,当 且
且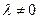 时,数列
时,数列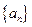 是等比数列,故数列
是等比数列,故数列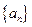 的前
的前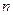 项和
项和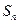

(3)若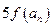 是
是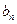 与
与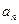 的等差中项,则
的等差中项,则

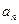 ,从而
,从而

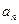 ,得
,得
 ,因
,因 是关于
是关于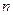 的减函数,所以当
的减函数,所以当 ,即
,即 时,
时,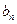 随
随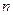 的增大而减小,此时最小值为
的增大而减小,此时最小值为 ,当
,当 ,即
,即 时,
时,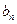 随
随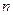 的增大而增大,此时最小值为
的增大而增大,此时最小值为 ,又
,又
 ,所以
,所以
 ,即数列
,即数列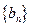 中
中 最小,为
最小,为
 :解得
:解得 ,故
,故
(2)因
 ,当
,当 时,
时, ,所以
,所以 ,又
,又 ,满足上式
,满足上式 ,当
,当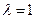 时,
时, ,当
,当 且
且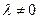 时,数列
时,数列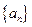 是等比数列,故数列
是等比数列,故数列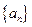 的前
的前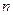 项和
项和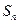

(3)若
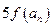 是
是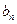 与
与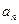 的等差中项,则
的等差中项,则

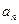 ,从而
,从而

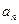 ,得
,得
 ,因
,因 是关于
是关于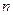 的减函数,所以当
的减函数,所以当 ,即
,即 时,
时,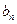 随
随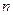 的增大而减小,此时最小值为
的增大而减小,此时最小值为 ,当
,当 ,即
,即 时,
时,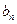 随
随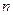 的增大而增大,此时最小值为
的增大而增大,此时最小值为 ,又
,又
 ,所以
,所以
 ,即数列
,即数列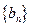 中
中 最小,为
最小,为
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
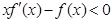 ,对任意正数a,b,若a<b,则必有( )
,对任意正数a,b,若a<b,则必有( )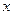 天的总销量
天的总销量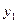 (千克)与
(千克)与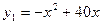 ;乙级干果从开始销售至销售的第
;乙级干果从开始销售至销售的第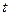 天的总销量
天的总销量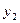 (千克)与
(千克)与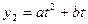 ,且乙级干果的前三天的销售量的情况见下表:
,且乙级干果的前三天的销售量的情况见下表:
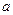 、
、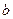 的值;
的值; 的一个正数零点附近的函数值用二分法计算,其参
的一个正数零点附近的函数值用二分法计算,其参
 的一个近似根(精确到0.1)为
的一个近似根(精确到0.1)为  .
. 的图象;
的图象; 
 的图像大致是( )
的图像大致是( )
 ,函数
,函数 有最小值,则不等式
有最小值,则不等式

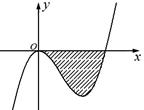
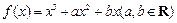 的图象如图所示,它与直线
的图象如图所示,它与直线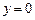 在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为
在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为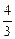 ,则
,则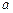 的值为
的值为