题目内容
17.$\int_1^2{(2x+k)}$dx=4,则k=1.分析 根据定积分的计算法则计算,得到关于k的方程,解得即可.
解答 解:$\int_1^2{(2x+k)}$dx=(x2+kx)|${\;}_{1}^{2}$=(4+2k)-(1+k)=3+k=4,
解得k=1,
故答案为:1.
点评 本题考查了定积分的计算,关键是求出原函数,属于基础题

练习册系列答案
相关题目
2.已知向量$\overrightarrow a=(3,1)$,$\overrightarrow b=(1,3),\overrightarrow c=(k,7)$,若$(2\overrightarrow a-\overrightarrow c)∥\overrightarrow b$,则k=( )
| A. | 21 | B. | $\frac{23}{3}$ | C. | $\frac{13}{3}$ | D. | -9 |
6.已知集合A={x|-3≤1-2x<3},集合B={x|y=lg(x-1)},则A∩B等于( )
| A. | {x|-2<x≤1} | B. | {x|1<x<2} | C. | {x|1<x≤2} | D. | {x|-1≤x<2} |
7.下列函数中,满足“f(x+y)=f(x)+f(y)”的单调递减函数是( )
| A. | f(x)=x2(x≥0) | B. | f(x)=-2x | C. | f(x)=3x-2 | D. | f(x)=x3 |
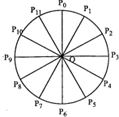 如图圆O是半径为1的圆,点PO、P1、P2…、P11将圆12等分,则$\overrightarrow{O{P}_{0}}$$•\overrightarrow{O{P}_{i}}$(i=0,1,2,3,…,11)的取值集合是{-1,-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,0,$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,1}.
如图圆O是半径为1的圆,点PO、P1、P2…、P11将圆12等分,则$\overrightarrow{O{P}_{0}}$$•\overrightarrow{O{P}_{i}}$(i=0,1,2,3,…,11)的取值集合是{-1,-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,0,$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,1}.