题目内容
已知三棱锥S-ABC中,侧棱SA、SB、SC两两垂直,若将此三棱锥沿侧棱展成平面图形恰好可以形成一个边长为a的正方形.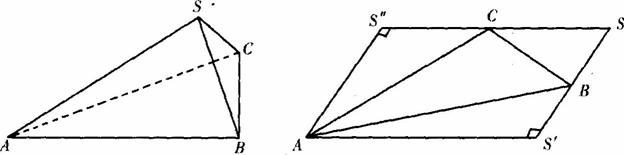
(Ⅰ)求证:顶点S在底面ABC的射影O是底面△ABC的垂心;
(Ⅱ)求SC与底面ABC所成的角的大小.
解:(Ⅰ)作SO⊥平面ABC,连接AO、BO,
因为侧棱SA、SB、SC两两垂直,易证SA⊥平面SBC、SB⊥平面SAC、SC⊥平面SAB.
所以SA⊥BC,由三垂线定理的逆定理,AO⊥BC,同理可证BO⊥AC.所以O为高线的交点,即为△ABC垂心.
(Ⅱ)连接CO,则∠SCO为SC与底面ABC所成的角.
由于三棱锥的展开图成边长为a的正方形,则B、C分别为SS′和SS″的中点,即SB=SC=![]() ,所以SA=a,AB=AC=
,所以SA=a,AB=AC=![]() a,BC=
a,BC=![]() a.
a.
延长CO交AB于D,连接SD.因为CO⊥AB,根据三垂线定理,SD⊥AB
在三角形SAB中,∠ASB=90°,SB=![]() ,SA=a,AB=
,SA=a,AB=![]() a,所以SD=
a,所以SD=![]() a
a
所以,tan∠SCO=tan∠SCD=![]() =
=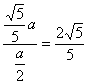
即SC与底面ABC所成的角的大小为arctan![]()

练习册系列答案
相关题目