题目内容
【题目】在![]() 中,
中, ![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() .
.
(1)求角![]() 的大小;
的大小;
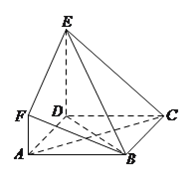
(2)若![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,求
的中点,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由已知,利用正弦定理可得![]() a2=
a2=![]() b2+
b2+![]() c2-2b,再利用余弦定理即可得出cosA,结合A的范围即可得解A的值.
c2-2b,再利用余弦定理即可得出cosA,结合A的范围即可得解A的值.
(2)△ABC中,先由正弦定理求得AC的值,再由余弦定理求得AB的值,△ABD中,由余弦定理求得BD的值.
试题解析:
(1)因为![]() asin A=(
asin A=(![]() b-c)sin B+(
b-c)sin B+(![]() c-b)·sin C,
c-b)·sin C,
由正弦定理得![]() a2=(
a2=(![]() b-c)b+(
b-c)b+(![]() c-b)c,
c-b)c,
整理得![]() a2=
a2=![]() b2+
b2+![]() c2-2bc,
c2-2bc,
由余弦定理得cos A=![]() =
=![]() =
=![]() ,
,
因为A∈(0,π),所以A=![]() .
.
(2)由cos B=![]() ,得sin B=
,得sin B=![]() =
=![]() =
=![]() ,
,
所以cos C=cos[π-(A+B)]=-cos(A+B)=-![]() =-
=-![]() ,
,
由正弦定理得b=![]() =
=![]() =2,
=2,
所以CD=![]() AC=1,
AC=1,
在△BCD中,由余弦定理得BD2=(![]() )2+12-2×1×
)2+12-2×1×![]() ×
×![]() =13,
=13,
所以BD=![]() .
.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案【题目】某市高中全体学生参加某项测评,按得分评为![]() 两类(评定标准见表1).根据男女学生比例,使用分层抽样的方法随机抽取了10000名学生的得分数据,其中等级为
两类(评定标准见表1).根据男女学生比例,使用分层抽样的方法随机抽取了10000名学生的得分数据,其中等级为![]() 的学生中有40%是男生,等级为
的学生中有40%是男生,等级为![]() 的学生中有一半是女生.等级为
的学生中有一半是女生.等级为![]() 和
和![]() 的学生统称为
的学生统称为![]() 类学生,等级为
类学生,等级为![]() 和
和![]() 的学生统称为
的学生统称为![]() 类学生.整理这10000名学生的得分数据,得到如图2所示的频率分布直方图,
类学生.整理这10000名学生的得分数据,得到如图2所示的频率分布直方图,
类别 | 得分( | |
|
|
|
|
| |
|
|
|
|
| |
表1
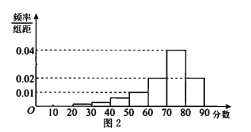
(I)已知该市高中学生共20万人,试估计在该项测评中被评为![]() 类学生的人数;
类学生的人数;
(Ⅱ)某5人得分分别为45,50,55,75,85.从这5人中随机选取2人组成甲组,另外3人组成乙组,求“甲、乙两组各有1名![]() 类学生”的概率;
类学生”的概率;
(Ⅲ)在这10000名学生中,男生占总数的比例为51%, ![]() 类女生占女生总数的比例为
类女生占女生总数的比例为![]() ,
, ![]() 类男生占男生总数的比例为
类男生占男生总数的比例为![]() ,判断
,判断![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)