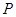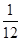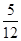题目内容
一个袋中装有10个大小相同的小球.其中白球5个、黑球4个、红球1个.
(1)从袋中任意摸出2个球,求至少得到1个白球的概率;
(2)从袋中任意摸出3个球,记得到白球的个数为 ,求随机变量
,求随机变量 的数学期望
的数学期望 .
.
【答案】
(1)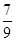 ;(2)
;(2)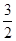
【解析】
试题分析:(1)古典概型,“至少得到一个白球”分为“恰好1个白球”和“两个都是白球”两类,也可以先求它的对立事件“两个都不是白球的概率”;(2)先考虑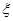 所有可能的取值,再求出
所有可能的取值,再求出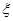 各个取值的概率,最后求出
各个取值的概率,最后求出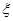 的数学期望.
的数学期望.
试题解析:(1)解:记“从袋中任意摸出两个球,至少得到一个白球”为事件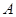 ,
,
则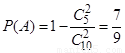 .
3分
.
3分
(2)随机变量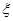 的取值为0,1,2,3,
4分
的取值为0,1,2,3,
4分
由于 6分
6分 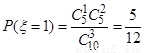 , 8分
, 8分
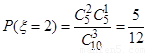 , 10分
, 10分 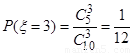 , 12分
, 12分
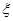 的分布列是
的分布列是
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
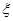 的数学期望
的数学期望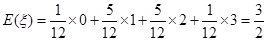 .
13分
.
13分
考点:离散型随机变量的概率分布、离散型随机变量的数学期望.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目