题目内容
若存在常数k和b,使得函数f(x)和g(x)在它们的公共定义域上的任意实数x分别满足:f(x)≥kx+b和g(x)≤kx+b,则称直线l:y=kx+b为函数f(x)和g(x)的“隔离直线”.已知f(x)=x2,g(x)=2elnx.(I)求F(x)=f(x)-g(x)的极值;
(II)函数f(x)和g(x)是否存在隔离直线?若存在,求出此隔离直线的方程,若不存在,请说明理由.
分析:(1)根据求导公式,求出函数的导数,根据导数判断函数的单调性并求极值
(2)由(1)可知,函数f(x)和g(x)的图象在x=
处有公共点,因此存在f(x)和g(x)的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k.则隔离直线方程为y-e=k(x-
,即y=kx-k
+e,构造函数,求出函数函数的导数,根据导数求出函数的最值
(2)由(1)可知,函数f(x)和g(x)的图象在x=
| e |
| e |
| e |
解答:解:(1)∵F(x)=f(x)-g(x)=x2-2clnx(x>0),
∴F′(x)=2x-
=(2x2-2c)/x=
令F′(X)=0,得x=
,
当0<x<
时,F′(X)<0,X>
时,F′(x)>0
故当x=
时,F(x)取到最小值,最小值是0
(2)由(1)可知,函数f(x)和g(x)的图象在x=
处有公共点,因此存在f(x)和g(x)的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k.则隔离直线方程为y-e=k(x-
,即y=kx-k
+e
由f(x)≥kx-k
+e(x?R),可得x2-kx-k
+e,
由f(x)≥kx-k
+e(x?R),可得x2-kx+k
-e≥0当x?R恒成立,
则△=k2-4k
+4e=(k-2
)2≤0,只有k=2
,此时直线方程为:y=2
x-e,
下面证明g(x)≤2
x-eexx>0时恒成立
令G(x)=2
x-e-g(x)=2
x-e-2elnx,
G′(X)=2
-
=(2
x-2c)/x=2
(x-
)/x,
当x=
时,G′(X)=0,当0<x<
时G′(X)>0,
则当x=
时,G(x)取到最小值,极小值是0,也是最小值.
所以G(x)=2
x-e-g(x)≥0,则g(x)≤2
x-e当x>0时恒成立.
∴函数f(x)和g(x)存在唯一的隔离直线y=2
x-e
∴F′(x)=2x-
| 2c |
| x |
2(x-
| ||||
| x |
令F′(X)=0,得x=
| e |
当0<x<
| e |
| e |
故当x=
| e |
(2)由(1)可知,函数f(x)和g(x)的图象在x=
| e |
| e |
| e |
由f(x)≥kx-k
| e |
| e |
由f(x)≥kx-k
| e |
| e |
则△=k2-4k
| e |
| c |
| e |
| e |
下面证明g(x)≤2
| e |
令G(x)=2
| e |
| e |
G′(X)=2
| c |
| 2c |
| x |
| c |
| c |
| e |
当x=
| e |
| e |
则当x=
| e |
所以G(x)=2
| e |
| e |
∴函数f(x)和g(x)存在唯一的隔离直线y=2
| e |
点评:考查函数的求导,利用导数求最值,属于简单题,主要做题要仔细.

练习册系列答案
相关题目
 和
和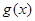 对其定义域上的任意实数x恒有:
对其定义域上的任意实数x恒有: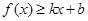 和
和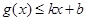 ,则称直线
,则称直线 为
为 ,则可推知
,则可推知 的“隔离直线”方程为 ▲
的“隔离直线”方程为 ▲
 .
.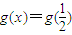 ;
;