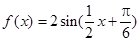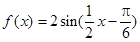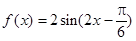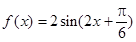题目内容
设函数 ·
·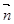 ,其中向量
,其中向量 ,
,
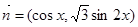 ,
,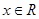 。
。
(1)求f (x)的最小正周期与单调递减区间;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,已知f (A) =2,b = 1,
△ABC的面积为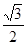 ,求△ABC 外接圆半径R的值。
,求△ABC 外接圆半径R的值。
 ·
·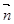 ,其中向量
,其中向量 ,
,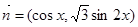 ,
,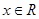 。
。(1)求f (x)的最小正周期与单调递减区间;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,已知f (A) =2,b = 1,
△ABC的面积为
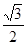 ,求△ABC 外接圆半径R的值。
,求△ABC 外接圆半径R的值。(1) ,
, (2)R=1
(2)R=1
 ,
, (2)R=1
(2)R=1本试题主要是考查了三角函数的性质和解三角形的综合运用。
(1)先根据向量的数量积运算表示出函数f(x),再由二倍角公式和两角和与差的公式进行化简,根据T公式可求得最小正周期,再由正弦函数的单调性可求得单调递增区间.
(2)由f(A) = 2,得 ,
,
在△ABC中,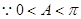 ,
,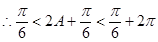 ,
,
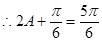 ,解得
,解得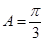 ,表示面积得到。
,表示面积得到。
解:(1)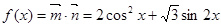
 ,
,
∴函数f(x)的最小正周期 。............3分
。............3分
令
 ,解得
,解得 。
。
∴函数f(x)的单调递减区间是 。........... 6分
。........... 6分
(2)由f(A) = 2,得 ,
,
在△ABC中,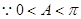 ,
,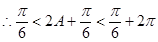 ,
,
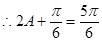 ,解得
,解得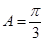 。
。
又 ,解得c = 2,
,解得c = 2,
△ABC中,由余弦定理得: ,∴a =
,∴a = 
根据正弦定理 ,得R=1。............12分
,得R=1。............12分
(1)先根据向量的数量积运算表示出函数f(x),再由二倍角公式和两角和与差的公式进行化简,根据T公式可求得最小正周期,再由正弦函数的单调性可求得单调递增区间.
(2)由f(A) = 2,得
 ,
,在△ABC中,
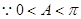 ,
,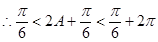 ,
,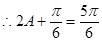 ,解得
,解得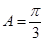 ,表示面积得到。
,表示面积得到。解:(1)
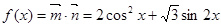
 ,
,∴函数f(x)的最小正周期
 。............3分
。............3分令

 ,解得
,解得 。
。∴函数f(x)的单调递减区间是
 。........... 6分
。........... 6分(2)由f(A) = 2,得
 ,
,在△ABC中,
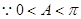 ,
,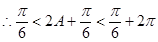 ,
,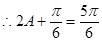 ,解得
,解得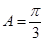 。
。又
 ,解得c = 2,
,解得c = 2,△ABC中,由余弦定理得:
 ,∴a =
,∴a = 
根据正弦定理
 ,得R=1。............12分
,得R=1。............12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 )(A>0,0<
)(A>0,0<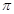 ),x
),x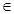 R的最大值是1,其图像经过点M
R的最大值是1,其图像经过点M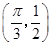 .
.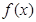 的解析式;
的解析式; 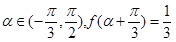 ,求
,求 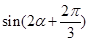 的值.
的值.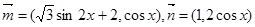 ,设函数
,设函数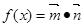 。
。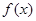 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;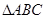 中,
中,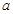 、
、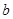 、
、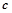 分别是角
分别是角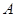 、
、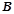 、
、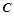 的对边,若
的对边,若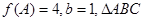 的面积为
的面积为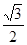 ,求
,求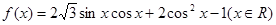 。
。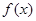 的最小正周期及在区间
的最小正周期及在区间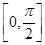 上的最大值和最小值;
上的最大值和最小值;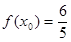 ,
,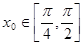 ,求
,求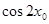 的值。
的值。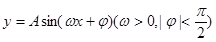 的图象按
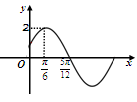
的图象按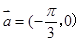 平移后得到y=f(x)的图象如图,则
平移后得到y=f(x)的图象如图,则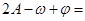
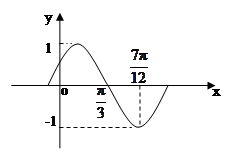
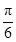
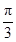
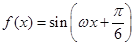 的导函数
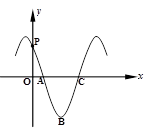
的导函数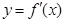 的部分图像如图所示:图象与
的部分图像如图所示:图象与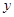 轴交点
轴交点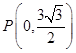 ,与x轴正半轴的两交点为A、C,B为图象的最低点 ,则
,与x轴正半轴的两交点为A、C,B为图象的最低点 ,则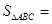 ___ ___ .
___ ___ .
 的图象如图所示,则
的图象如图所示,则 .
.
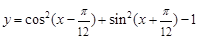 的最小正周期为( ).
的最小正周期为( ).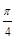
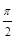
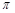
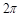
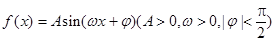 的部分图象如下图所示,则函数
的部分图象如下图所示,则函数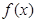 的解析式为
的解析式为