题目内容
(本小题满分12分)
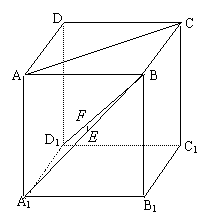 在棱长为1的正方体
在棱长为1的正方体![]() 中,
中,![]() 为
为![]() 上的点,且满足
上的点,且满足![]() ,
,![]() 为
为![]() 上的点,且满足
上的点,且满足![]() 。
。
(1)求异面直线![]() 与AC所成的角的大小;
与AC所成的角的大小;
(2)求证:![]()
(3)求证:![]() ∥平面
∥平面![]()
(本小题满分12分)
解:(1)连结![]() 、
、![]() ,则
,则![]() //AC,
//AC,
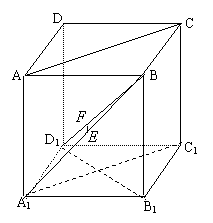 则
则![]() 是异面直线
是异面直线![]() 与AC所成的角 ……2分
与AC所成的角 ……2分
在正![]() 中,
中, ![]() =60
=60![]()
![]() 异面直线
异面直线![]() 与AC所成的角为60
与AC所成的角为60![]() ……4分
……4分
(2)连结![]() ,因为四边形
,因为四边形![]() 为正方形,
为正方形,
所以![]() ………6分
………6分
又![]() 是
是![]() 在平面
在平面![]() 内的射影,由三垂线定理得:
内的射影,由三垂线定理得: ![]() ……8分
……8分
(3)∵![]() 为
为![]() 上的点,且满足
上的点,且满足![]() ,∴
,∴![]() 为
为![]() 的中点。
的中点。
又∵![]() 为
为![]() 上的点,且满足
上的点,且满足![]() ,∴
,∴![]() 为
为![]() 的中点……10分
的中点……10分
在![]() 中,
中,![]() ∥
∥![]() ,又在正方体
,又在正方体![]() 中,
中,![]() ∥
∥![]() ,
,![]() ∥
∥![]()
又![]() ,而
,而![]()
![]() ,所以由线面平行的判定定理有
,所以由线面平行的判定定理有![]() ∥平面
∥平面![]() ……12分
……12分

练习册系列答案
相关题目