题目内容
 在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.
在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.(Ⅰ)求证:AC⊥平面FBC;
(Ⅱ)线段ED上是否存在点Q,使平面EAC⊥平面QBC?证明你的结论.
分析:(I)利用余弦定理和勾股定理的逆定理可得AC⊥BC,再利用已知AC⊥FB和线面垂直的判定定理即可证明;
(II)通过建立空间直角坐标系,利用两个平面的法向量是否垂直即可.
(II)通过建立空间直角坐标系,利用两个平面的法向量是否垂直即可.
解答:(Ⅰ)证明:∵AB=2BC,∠ABC=60°,
在△ABC中,由余弦定理可得AC2=AB2+BC2-2AB•BCcos60°=3BC2,
∴AC2+BC2=4BC2=AB2,∴∠ACB=90°.
∴AC⊥BC.
又∵AC⊥FB,FB∩BC=B,
∴AC⊥平面FBC.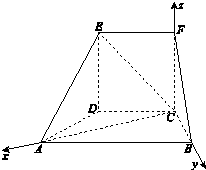
(Ⅱ)
线段ED上不存在点Q,使平面EAC⊥平面QBC.
证明如下:
因为AC⊥平面FBC,所以AC⊥FC.
因为CD⊥FC,所以FC⊥平面ABCD.
所以CA,CF,CB两两互相垂直,如图建立的空间直角坐标系C-xyz.
在等腰梯形ABCD中,可得 CB=CD.
设BC=1,所以C(0,0,0),A(
,0,0),B(0,1,0),D(
,-
,0),E(
,-
,1).
所以
=(
,-
,1),
=(
,0,0),
=(0,1,0).
设平面EAC的法向量为
=(x,y,z),则
,
所以
取z=1,得
=(0,2,1).
假设线段ED上存在点Q,设Q(
,-
,t)(0≤t≤1),所以
=(
,-
,t).
设平面QBC的法向量为
=(a,b,c),则
所以
取c=1,得
=(-
,0,1).
要使平面EAC⊥平面QBC,只需
•
=0,
即 -
t×0+0×2+1×1=0,此方程无解.
所以线段ED上不存在点Q,使平面EAC⊥平面QBC.
在△ABC中,由余弦定理可得AC2=AB2+BC2-2AB•BCcos60°=3BC2,
∴AC2+BC2=4BC2=AB2,∴∠ACB=90°.
∴AC⊥BC.
又∵AC⊥FB,FB∩BC=B,
∴AC⊥平面FBC.

(Ⅱ)
线段ED上不存在点Q,使平面EAC⊥平面QBC.
证明如下:
因为AC⊥平面FBC,所以AC⊥FC.
因为CD⊥FC,所以FC⊥平面ABCD.
所以CA,CF,CB两两互相垂直,如图建立的空间直角坐标系C-xyz.
在等腰梯形ABCD中,可得 CB=CD.
设BC=1,所以C(0,0,0),A(
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
所以
| CE |
| ||
| 2 |
| 1 |
| 2 |
| CA |
| 3 |
| CB |
设平面EAC的法向量为
| n |
|
所以
|
| n |
假设线段ED上存在点Q,设Q(
| ||
| 2 |
| 1 |
| 2 |
| CQ |
| ||
| 2 |
| 1 |
| 2 |
设平面QBC的法向量为
| m |
|
所以
|
| m |
| 2t | ||
|
要使平面EAC⊥平面QBC,只需
| m |
| n |
即 -
| 2 | ||
|
所以线段ED上不存在点Q,使平面EAC⊥平面QBC.
点评:本题综合考查了线面、面面垂直的判定定理与性质定理、通过距离空间直角坐标系利用两个平面的法向量解决面面垂直等基础知识与基本技能,考查了空间想象能力、推理能力和计算能力.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
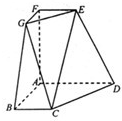 在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC.
在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC.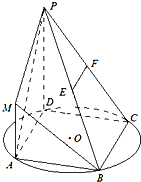 在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP=
在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP= (2012•朝阳区一模)在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1,
(2012•朝阳区一模)在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1,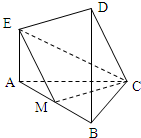 在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE=2,M是AB的中点.