题目内容
在数列{an}中,a1=2,a4=8,且满足an+2=2an+1-an(n∈N*)
(1)求数列{an}的通项公式
(2)设bn=2n-1·an,求数列{bn}的前n项和sn
【答案】
(1)an=2+2(n—1)=2n
(2)bn=2n-1·2n=n·2n
sn=(n-1)2n+1+2
【解析】解:(1)∵an+2=2an+1-an(n∈N*)
∴an+an+2=2an+1
∴{an}为等差数列
设公差为d,由题意得8=2+3d,∴d=2 ∴an=2+2(n—1)=2n
(2)∵bn=2n-1·2n=n·2n
∴sn=b1+b2+b3+…+bn=1·21+2·22+3·23+…+n·2n ①
∴2sn=1·22+2·23+…(n—1)·2n+n·2n+1 ②
①—②得-sn=21+22+23+…+2n—n·2n+1=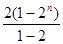 -n·2n+1=2n+1-2- n·2n+1=(1-n)2n+1-2
-n·2n+1=2n+1-2- n·2n+1=(1-n)2n+1-2
∴sn=(n-1)2n+1+2

练习册系列答案
相关题目
在数列(an)中,an=2n-7,则当前n项和取得最小值时的n的等于( )
| A、3 | B、4 | C、3或4 | D、4或5 |
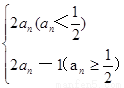 ,若a1=
,若a1=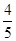 ,则a2012的值为
,则a2012的值为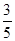 . B、
. B、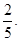 D、
D、