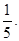题目内容
在数列(an)中,an=2n-1,若一个7行12列的矩阵的第i行第j列的元素cij=ai•aj+ai+aj(i=1,2,…,7;j=1,2,…,12),则该矩阵元素能取到的不同数值的个数为( )
| A.18 | B.28 | C.48 | D.63 |
该矩阵的第i行第j列的元素cij=ai•aj+ai+aj=(2i-1)(2j-1)+2i-1+2j-1=2i+j-1(i=1,2,…,7;j=1,2,…,12),
当且仅当:i+j=m+n时,aij=amn(i,m=1,2,…,7;j,n=1,2,…,12),
因此该矩阵元素能取到的不同数值为i+j的所有不同和,其和为2,3,…,19,共18个不同数值.
故选A.
当且仅当:i+j=m+n时,aij=amn(i,m=1,2,…,7;j,n=1,2,…,12),
因此该矩阵元素能取到的不同数值为i+j的所有不同和,其和为2,3,…,19,共18个不同数值.
故选A.

练习册系列答案
相关题目
在数列(an)中,an=2n-7,则当前n项和取得最小值时的n的等于( )
| A、3 | B、4 | C、3或4 | D、4或5 |
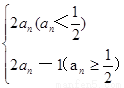 ,若a1=
,若a1=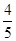 ,则a2012的值为
,则a2012的值为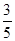 . B、
. B、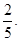 D、
D、