题目内容
若关于x的方程4x-k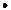 2x+k+3=0无实数解,求k的取值范围。
2x+k+3=0无实数解,求k的取值范围。
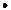 2x+k+3=0无实数解,求k的取值范围。
2x+k+3=0无实数解,求k的取值范围。
-3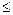 k<6
k<6
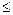 k<6
k<6设t=2x>0,原方程即为t2-kt+k+3=0(t>0)
原方程无解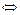 t2-kt+k+3=0无正解
t2-kt+k+3=0无正解
(1)t2-kt+k+3=0无解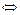
 =k2-4(k+3)= k2-4k-12<0
=k2-4(k+3)= k2-4k-12<0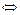 -2<k<6
-2<k<6
(2) t2-kt+k+3=0有两负解或一负解一解为0
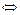
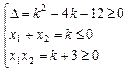
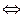 -3
-3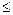 k
k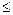 -2
-2
综上-3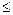 k<6
k<6
原方程无解
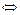 t2-kt+k+3=0无正解
t2-kt+k+3=0无正解(1)t2-kt+k+3=0无解
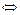
 =k2-4(k+3)= k2-4k-12<0
=k2-4(k+3)= k2-4k-12<0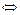 -2<k<6
-2<k<6(2) t2-kt+k+3=0有两负解或一负解一解为0
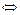
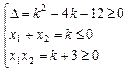
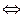 -3
-3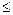 k
k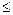 -2
-2综上-3
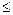 k<6
k<6
练习册系列答案
相关题目
 ,
, ,
, ,求证:
,求证: <-1;
<-1; 在(0,1)内有两个实根.
在(0,1)内有两个实根. 的图象所围成的图形的面积为
的图象所围成的图形的面积为 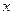 的方程
的方程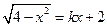 只有一个实数根,则
只有一个实数根,则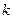 的取值范围为( )
的取值范围为( )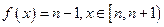 ,
,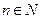 ,函数
,函数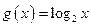 ,则方程
,则方程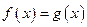 中实数根的个数是
中实数根的个数是 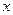 的方程
的方程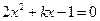
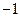 ,求另一个根及
,求另一个根及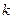 值.
值. 的实数解落在的区间是 ( )
的实数解落在的区间是 ( )



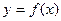 的定义域和值域都是
的定义域和值域都是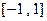 (其图像如下图所示),
(其图像如下图所示),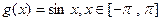 .定义:当
.定义:当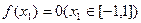 且
且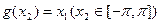
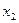 是方程
是方程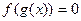 的一个实数根.则方程
的一个实数根.则方程 .
.