Question

【题目】若实数满足，则称比接近

（1）若4比接近0，求的取值范围；

（2）对于任意的两个不等正数，求证：比接近；

（3）若对于任意的非零实数，实数比接近，求的取值范围

Answer 1

【答案】（1）；（2）证明见解析；（3）

【解析】

（1）由题意得：|x2﹣3x|＞4，则x2﹣3x＞4或x2﹣3x＜﹣4，由此求得x的范围．

（2）根据，且，化简||﹣|a+b﹣2|的结果大于零，可得a+b比接近．

（3）由题意对于x∈R，x≠0恒成立，分类讨论求得|x1|的最小值，可得|a+1|的范围，从而求得a的范围．

解：（1）由题意得：|x2﹣3x|＞4，则x2﹣3x＞4或x2﹣3x＜﹣4，

由x2﹣3x＞4，求得x＞4或x＜﹣1；由x2﹣3x＜﹣4，求得x无解．

所以x取值范围为（﹣∞，﹣1）∪（4，+∞）．

（2）因为a，b＞0且a≠b，所以，且，

所以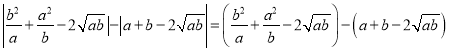

，

则，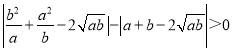

即a+b比接近．　　　　　　　　　　　　　　　　

（3）由题意：对于x∈R，x≠0恒成立，

当x＞0时，，当x＝2时等号成立，

当x＜0时，则﹣x＞0，，当x＝﹣2时等号成立，所以，则，

综上．

故由|a+1|＜3，求得﹣4＜a＜2，即a取值范围为（﹣4，2）．