题目内容
已知圆的方程为C:(x-2)2+(y+3)2=9,求圆上的点到已知直线L:ax+by+c=0(a2+b2≠0)的最大距离和最小距离.请设计一个算法程序框图,并写出算法程序.
分析:求圆上的点到已知直线L:ax+by+c=0(a2+b2≠0)的最大距离和最小距离需分离讨论,故用选择结构画出算法程序框图,然后根据程序框图写出算法程序即可.
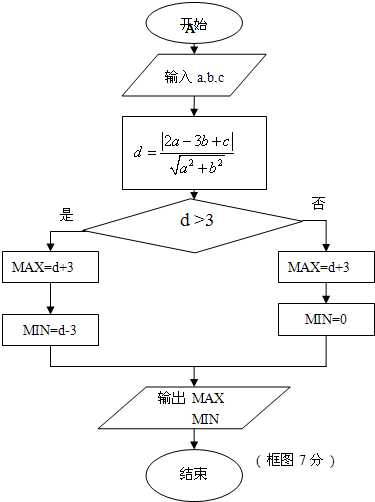
解答:解:求圆C上的点到直线L距离的最大值与最小值的程序框图,运算程序如下:
 INPUT a,b,c
INPUT a,b,c
r=ABS(2*a-3*b+c)
s=SQR(a*a+b*b)
d=r/s
IF d>3 THEN
MAX=d+3
MIN=d-3
ELSE
MAX=d+3
MIN=0
END IF
PRINT“MAX=“;MAX
PRINT“MIN=“;MIN
END
 INPUT a,b,c
INPUT a,b,cr=ABS(2*a-3*b+c)
s=SQR(a*a+b*b)
d=r/s
IF d>3 THEN
MAX=d+3
MIN=d-3
ELSE
MAX=d+3
MIN=0
END IF
PRINT“MAX=“;MAX
PRINT“MIN=“;MIN
END
点评:本题考查了程序框图中的条件结构,条件结构有两个路径,满足条件执行一个路径,不满足条件,执行另一个路径,解答本题的关键弄清判断框的条件,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知圆的方程为x2+y2+2(a-1)x+a2-4a+1=0(0<a<
),则点(-1,-1)的位置是( )
| 1 |
| 2 |
| A、在圆上 | B、在圆内 |
| C、在圆外 | D、不能确定 |
已知圆的方程为x2+y2=4,若抛物线过点A(-1,0),B(1,0),且以圆的切线为准线,则抛物线的焦点轨迹方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|