题目内容
已知y=loga(2-ax),在［0,1］上是x的减函数，求a的取值范围.
1<a<2..
（1）首先设u=2-ax,当a∈(0,1),x∈［0,1］时，u是减函数，y=logau是u的减函数，则函数y=loga(2-ax)在［0,1］上是增函数，不合题意.
（2）当a∈(1,+∞),x∈［0,1］时，u是x的减函数，y=logau是u的增函数，则函数y=loga(2-ax)在［0,1］上是减函数，但2-ax>0,在x∈［0,1］时必须恒成立，
有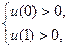
得a<2,故1<a<2.
（2）当a∈(1,+∞),x∈［0,1］时，u是x的减函数，y=logau是u的增函数，则函数y=loga(2-ax)在［0,1］上是减函数，但2-ax>0,在x∈［0,1］时必须恒成立，
有
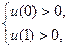得a<2,故1<a<2.
练习册系列答案
相关题目
下列不等式一定成立的是（ ）
；
；
；
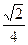
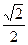
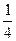
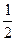
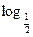x，x∈(0,8)的值域是_________________.
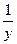）+(x2+
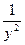)+(x3+
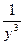)+…+(x2 010+
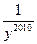)的值等于_________________.
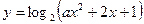的值域为
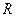，则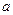
的范围为__________。
（ ）
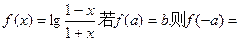