题目内容
6.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),x∈R的最大值是1,且函数最大值与最小值间对应的横坐标最小距离为π,其图象经过点M($\frac{π}{3}$,$\frac{1}{2}$).(Ⅰ)求f(x)的解析式;
(Ⅱ)设f(α)=$\frac{2\sqrt{5}}{5}$,f(β+$\frac{π}{2}$)=-$\frac{\sqrt{10}}{10}$,α∈(0,$\frac{π}{2}$),β∈(0,$\frac{π}{2}$),求sinα,cosβ的值.
分析 (1)首先,根据已知,得到A=1,$\frac{T}{2}=π$,从而有T=$\frac{2π}{ω}$=2π,然后,将点M($\frac{π}{3}$,$\frac{1}{2}$)代入,即可得到结果;
(2)根据(1),得到cosα=$\frac{2\sqrt{5}}{5}$,sinβ=$\frac{\sqrt{10}}{10}$,然后,结合同角三角函数基本关系式求解即可.
解答 解:(1)根据题意,得A=1,
∵函数最大值与最小值间对应的横坐标最小距离为π,
∴$\frac{T}{2}=π$,
∴T=$\frac{2π}{ω}$=2π,
∴ω=1.
∴f(x)=sin(x+φ),
将点M($\frac{π}{3}$,$\frac{1}{2}$)代入上述解析式,得.
f($\frac{π}{3}$)=sin($\frac{π}{3}$+φ)=$\frac{1}{2}$,0<φ<π,
∴φ=$\frac{π}{2}$,
∴f(x)=sin(x+$\frac{π}{2}$)=cosx.
(2)根据(1),得
f(α)=cosα=$\frac{2\sqrt{5}}{5}$,
f(β+$\frac{π}{2}$)=-$\frac{\sqrt{10}}{10}$,
∴cos($β+\frac{π}{2}$)=-sinβ=-$\frac{\sqrt{10}}{10}$,
∴sinβ=$\frac{\sqrt{10}}{10}$,
∵α∈(0,$\frac{π}{2}$),β∈(0,$\frac{π}{2}$),
∴sinα=$\sqrt{1-co{s}^{2}α}=\frac{\sqrt{5}}{5}$,
cosβ=$\sqrt{1-si{n}^{2}β}=\frac{3\sqrt{10}}{10}$.
点评 本题考查由y=Asin(ωx+φ)的部分图象确定解析式、函数y=Asin(ωx+φ)的图象变换,考查函数方程思想、数形结合思想.

 阅读快车系列答案
阅读快车系列答案| A. | 2x+1 | B. | 2x-1 | C. | 2x-3 | D. | 2x+7 |
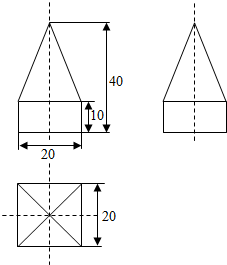 如图所示为一个多面组合体的三视图(单位:cm)
如图所示为一个多面组合体的三视图(单位:cm)