题目内容
已知椭圆C: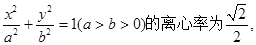 其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=
其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=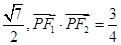 (O为坐标原点)。
(O为坐标原点)。
(1)求椭圆C的方程;
(2)过点 l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。
l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。
【答案】
(1)
(2)在y轴上存在定点M,使得以AB为直径的圆恒过这个点,
点M的坐标为(0,1)。
【解析】
试题分析:(1)设

因此所求椭圆的方程为: 5分
5分
(2)动直线l的方程为: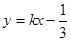 ,
,

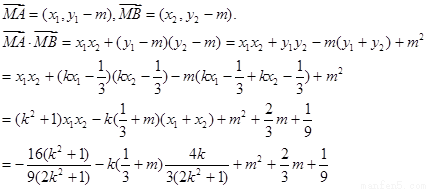
 10分
10分
由假设得对于任意的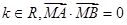 恒成立,
恒成立,
即
因此,在y轴上存在定点M,使得以AB为直径的圆恒过这个点,
点M的坐标为(0,1)。 13分
(以上答案仅供参考,其它解法酌情赋分)
考点:本题主要考查椭圆的标准方程,直线与椭圆的位置关系,平面向量的坐标运算。
点评:难题,求椭圆的标准方程,主要运用了椭圆的几何性质,注意明确焦点轴和a,b,c的关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(2)利用向量垂直,数量积为0,确定得到m的方程。

练习册系列答案
相关题目

 .若在线段MN上取一点R,使得
.若在线段MN上取一点R,使得 其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=
其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|= (O为坐标原点)。
(O为坐标原点)。 l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。
l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。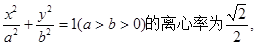 其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=
其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=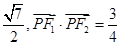 (O为坐标原点)。
(O为坐标原点)。 l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。
l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。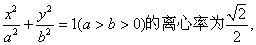 其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=
其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=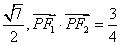 (O为坐标原点)。
(O为坐标原点)。 l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。
l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。