题目内容
已知椭圆C: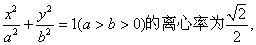 其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=
其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=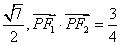 (O为坐标原点)。
(O为坐标原点)。
(1)求椭圆C的方程;
(2)过点 l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。
l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。
【答案】
(1)设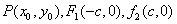
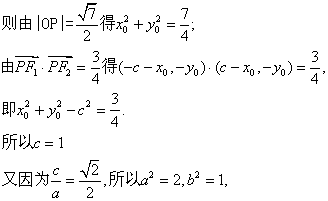
因此所求椭圆的方程为: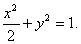 ………………5分
………………5分
(2)动直线l的方程为: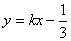 ,
,

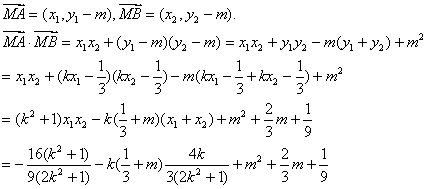
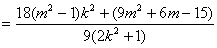 ………………10分
………………10分
由假设得对于任意的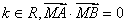 恒成立,
恒成立,
即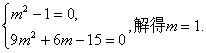
因此,在y轴上存在定点M,使得以AB为直径的圆恒过这个点,
点M的坐标为(0,1)。 ………………13分
(以上答案仅供参考,其它解法酌情赋分)

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目

 .若在线段MN上取一点R,使得
.若在线段MN上取一点R,使得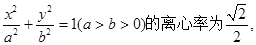 其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=
其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=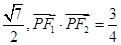 (O为坐标原点)。
(O为坐标原点)。 l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。
l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。 其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=
其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|= (O为坐标原点)。
(O为坐标原点)。 l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。
l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。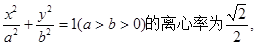 其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=
其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=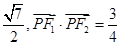 (O为坐标原点)。
(O为坐标原点)。 l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。
l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。