题目内容

18．已知球的表面积为64πcm2，用一个平面截球，使截面球的半径为2cm，则截面与球心的距离是2$\sqrt{3}$cm．

分析 先求出球的半径，再利用勾股定理，即可求出截面与球心的距离．

解答 解：球的表面积为64πcm2，则球的半径为4cm，
∵用一个平面截球，使截面球的半径为2cm，
∴截面与球心的距离是$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$cm．
故答案为：2$\sqrt{3}$．

点评 本题考查截面与球心的距离，考查球的表面积，求出球的半径是关键．

练习册系列答案
相关题目
8．定义在（-∞，0）∪（0，+∞）上的函数f（x），如果对于任意给定的等比数列{an}，{f（an）}，仍是等比数列，则称f（x）为“等比函数”．现有定义在（-∞，0）∪（0，+∞）上的如下函数：
①f（x）=3x；
②f（x）=x3； 
③f（x）=$\frac{2}{x}$； 
④f（x）=log2|x|．
则其中是“等比函数”的f（x）的序号为②③．
9．函数y=|x-1|的图象（　　）
A．关于直线x=1对称B．关于y轴对称
C．关于直线x=-1对称D．不是轴对称图形
6．下列命题中正确的是（　　）
A．命题“?x∈R，x2-x≤0”的否定是“?x∈R，x2-x≥0”
B．命题“p∧q为真”是命题“p∨q为真”的必要不充分条件
C．若“am2≤bm2，则a≤b”的否命题为真
D．若实数x，y∈[-1，1]，则点（x，y）所构成的平面区域为π
13．当m=6，n=3时，执行如图所示的程序框图，输出的S值为（　　）
A．6B．30C．120D．360
3．用0，1，2，3，4，5可以组成多少个无重复数字的比2000大的四位偶数？
10．若复数z满足1+zi=z （i为虚数单位），则z=$\frac{1+i}{2}$．
7．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为45°，且$\overrightarrow{a}$=（2，-2），|$\overrightarrow{b}$|=1，则|$\overrightarrow{a}$-$\overrightarrow{b}$|=（　　）
A．$\sqrt{2}$B．2C．$\sqrt{5}$D．3
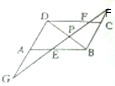18．如图，四边形ABCD是平行四边形，P是BD上任意一点，过P点的直线分别交AB，DC于E，F，交DA，BC的延长线于G，H．
（1）求证：PE•PG=PF•PH；
（2）当过P点的直线绕点P旋转到F，H，C重合时，请判断PE、PC、PG的关系，并给出证明．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网