题目内容
11．已知集合A={x|x2+2x-3＜0}，B={x|$\frac{x}{x-2}$＜0}，则A∩B=（ ）| A． | {x|x＜0} | B． | {x|x＞1} | C． | {x|0＜x≤1} | D． | {x|0＜x＜1} |
分析 求出A与B中不等式的解集确定出A与B，找出两集合的交集即可．
解答 解：由A中不等式变形得：（x-1）（x+3）＜0，
解得：-3＜x＜1，即A={x|-3＜x＜1}，
由B中不等式变形得：x（x-2）＜0，
解得：0＜x＜2，即B={x|0＜x＜2}，
则A∩B={x|0＜x＜1}，
故选：D．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
1．设a＞0，且a≠1，函数y=2+loga（x+2）的图象恒过定点P，则P点的坐标是（ ）
| A． | （-1，2） | B． | （2，-1） | C． | （3，-2） | D． | （3，2） |
6．
要建造一个容量为1200m3，深为6m的长方体无盖蓄水池，池壁的造价为95元/m2，池底的造价为135元/m2，求当水池的长在什么范围时，才能使水池的总造价不超过61200元（规定长大于等于宽）．
要建造一个容量为1200m3，深为6m的长方体无盖蓄水池，池壁的造价为95元/m2，池底的造价为135元/m2，求当水池的长在什么范围时，才能使水池的总造价不超过61200元（规定长大于等于宽）． 
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象向左平移$\frac{π}{3}$个单位，所得曲线的一部分如图所示，f（x）的周期为π，φ的值为-$\frac{π}{3}$．
20．
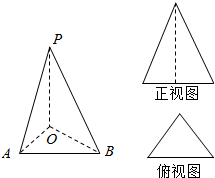若三棱锥P-ABC的正视图为如图所示边长为2的正三角形，俯视图为等腰直角三角形，则三棱锥的体积是（ ）
若三棱锥P-ABC的正视图为如图所示边长为2的正三角形，俯视图为等腰直角三角形，则三棱锥的体积是（ ）| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{2\sqrt{3}}{3}$ | D． | $\frac{4\sqrt{3}}{3}$ |