题目内容
【题目】给出下列五个命题,其中正确命题的个数为( )
①命题“![]() ,使得
,使得![]() ”的否定是“
”的否定是“![]() ,均有
,均有![]() ”;
”;
②若正整数![]() 和
和![]() 满足
满足![]() ,则
,则![]() ;
;
③在![]() 中 ,
中 ,![]() 是
是![]() 的充要条件;
的充要条件;
④一条光线经过点![]() ,射在直线
,射在直线![]() 上,反射后穿过点
上,反射后穿过点![]() ,则入射光线所在直线的方程为
,则入射光线所在直线的方程为![]() ;
;
⑤已知![]() 的三个零点分别为一椭圆、一双曲线、一抛物线的离心率,则
的三个零点分别为一椭圆、一双曲线、一抛物线的离心率,则![]() 为定值.
为定值.
A.2B.3C.4D.5
【答案】C
【解析】
①根据特称命题的否定的知识来判断;②根据基本不等式的知识来判断;③根据充要条件的知识来判断;④求得入射光线来判断;⑤利用抛物线的离心率判断.
①,命题“![]() ,使得
,使得![]() ”的否定是“
”的否定是“![]() ,均有
,均有![]() ”,故①错误.
”,故①错误.
②,由于正整数![]() 和
和![]() 满足
满足![]() ,
,![]() ,由基本不等式得
,由基本不等式得![]() ,当
,当![]() 即
即![]() 时等号成立,故②正确.
时等号成立,故②正确.
③,在![]() 中,由正弦定理得
中,由正弦定理得![]() ,即
,即![]() ,所以
,所以![]() 是
是![]() 的充要条件,故③正确.
的充要条件,故③正确.
④,设![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,则线段
,则线段![]() 中点为
中点为![]() ,则
,则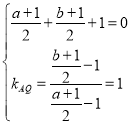 ,解得
,解得![]() ,所以
,所以![]() .所以入射光线为直线
.所以入射光线为直线![]() ,即
,即![]() ,化简得
,化简得![]() .故④正确.
.故④正确.
⑤,由于抛物线的离心率是![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() 为定值,所以⑤正确.
为定值,所以⑤正确.
故选:C

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
