题目内容
已知q是等比数列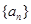 的公比,则“
的公比,则“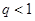 ”是“数列
”是“数列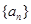 是递减数列”的( )
是递减数列”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】
D
【解析】
试题分析:若“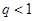 ”,则可取
”,则可取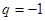 ,于是等比数列
,于是等比数列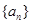 则成摆动数列而非递减数列,故不满足充分性;若“数列
则成摆动数列而非递减数列,故不满足充分性;若“数列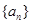 是递减数列”,则
是递减数列”,则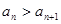 ,于是
,于是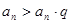 ,当
,当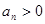 时可得
时可得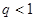 ;当
;当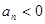 时可得
时可得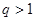 ,故不满足必要性.
,故不满足必要性.
考点:充分必要条件、等比数列的概念.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知{an}是等比数列,公比为q,设Sn=a1+a2Cn1+a3Cn2+…+an+1Cnn(其中n∈N*,n>2),且Tn=Cn0+Cn1+Cn2+…+Cnn(其中n∈N*,n>2),如果数列{
}有极限,则公比q的取值范围是( )
| Sn |
| Tn |
| A、-3<q≤1且q≠0 |
| B、-3<q<1且q≠0 |
| C、-1<q≤1且q≠0 |
| D、-1<q<1且q≠0 |
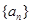 的公比,则“
的公比,则“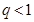 ”是“数列
”是“数列