题目内容
【题目】如图,矩形![]() 中,
中,![]() ,将
,将![]() 沿对角线
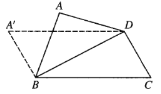
沿对角线![]() 向上翻折,若翻折过程中
向上翻折,若翻折过程中![]() 长度在
长度在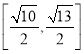 内变化,则点
内变化,则点![]() 所形成的运动轨迹的长度为__________.
所形成的运动轨迹的长度为__________.
【答案】![]()
【解析】
过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,根据题意得到点
,根据题意得到点![]() 在以点
在以点![]() 为圆心,
为圆心, ![]() 为半径的圆上运动,设当
为半径的圆上运动,设当![]() 运动到点
运动到点![]() 处时,
处时,![]() ,当
,当![]() 运动到点
运动到点![]() 处时,
处时,![]() ,根据勾股定理求出
,根据勾股定理求出![]() ,然后求出圆心角,根据弧长公式即可得到结果.
,然后求出圆心角,根据弧长公式即可得到结果.
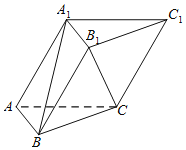
如图1:
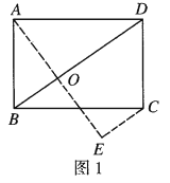
过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,
,
则易得![]() ,
,![]() .
.
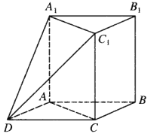
如图2:
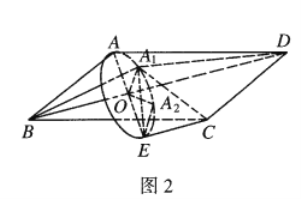
在图2中,由旋转的性质易得点![]() 在以点
在以点![]() 为圆心,
为圆心, ![]() 为半径的圆上运动,且
为半径的圆上运动,且![]() 垂直于圆
垂直于圆![]() 所在的平面,又因为
所在的平面,又因为![]() ,所以
,所以![]() 垂直于圆
垂直于圆![]() 所在的平面,
所在的平面,
设当![]() 运动到点
运动到点![]() 处时,
处时,![]() ,当
,当![]() 运动到点
运动到点![]() 处时,
处时,![]() ,
,
则有![]() ,则易得
,则易得![]() ,
,
则易得![]() 是以
是以![]() 为顶点的等腰直角三角形,
为顶点的等腰直角三角形,
在![]() 中,由余弦定理易得
中,由余弦定理易得![]() ,所以
,所以![]() ,所以
,所以![]() ,所以点
,所以点![]() 所形成的轨迹为半径为
所形成的轨迹为半径为![]() ,圆心角为
,圆心角为![]() 的圆弧,
的圆弧,
所以轨迹的长度为![]() .
.
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目