题目内容
(本小题10分)求经过两直线3x + 4y – 5 = 0与2x – 3y + 8 = 0的交点M,且与直线L1:2x + y + 5 = 0平行的直线L2的方程,并求L1与L2间的距离。
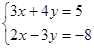 解得
解得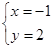
所以交点(-1,2)…………………………2分
易得L1的斜率为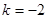 ……………………4分
……………………4分
∴直线L2的方程为 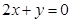 ………………………………6分
………………………………6分
由两平行线间的距离公式,得L1与L2间的距离为:
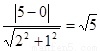 …………………………10分
…………………………10分
【解析】略

(本小题满分12分)
新能源汽车是指除汽油、柴油发动机之外所有其它能源汽车.包括燃料电池汽车、混合动力汽车、氢能源动力汽车和太阳能汽车等.其废气排放量比较低.为了配合我国“节能减排”战略,某汽车厂决定转型生产新能源汽车中的燃料电池汽车、混合动力和氢能源动力三类轿车,每类轿车均有标准型和豪华型两种型号,某月的产量如下表(单位:辆):
|
|
燃料电池轿车 |
混合动力轿车 |
氢能源动力轿车 |
|
标准型 |
100 |
200 |
|
|
豪华型 |
200 |
300 |
500 |
按类型分层抽样的方法在这个月生产的轿车中抽取100辆,其中有燃料电池轿车20辆.
(I) 求 的值.
的值.
(II) 用分层抽样的方法在氢能源动力轿车中抽取一个容量为7的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆标准型轿车的概率;
(Ⅲ) 用随机抽样的方法从混合动力标准型轿车中抽取10辆,经检测它们的得分如下:
9.3, 8.7, 9.1, 9.5, 8.8, 9.4, 9.0, 8.2,9.6, 8.4.
把这10辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.4的概率.
(本小题满分12分)
经统计,某大型商场一个结算窗口每天排队结算的人数及相应的概率如下:
|
排队人数 |
0~5 |
6~10 |
11~15 |
16~20 |
21~25 |
25人以上 |
|
概 率 |
0.1 |
0.15 |
0.25 |
0.25 |
0.2 |
0.05 |
(1)求每天不超过20人排队结算的概率;
(2)一周7天中,若有3天以上(含3天)出现超过15人排队结算的概率大于0.75,商场就需要增加结算窗口,试问该商场是否需要产加结算窗口?
 的函数,且销售量近似满足g(t)=80-2t,价格近似满足f(t)=20-
的函数,且销售量近似满足g(t)=80-2t,价格近似满足f(t)=20-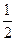 |t-10|.
|t-10|.  |t-10|.
|t-10|. 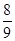 ,第二道工序检查合格的概率为
,第二道工序检查合格的概率为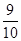 ,已知该厂每月生产3台这种仪器.
,已知该厂每月生产3台这种仪器.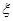 表示每月生产合格仪器的台数,求
表示每月生产合格仪器的台数,求