题目内容
（2013•广元二模）如图，在五面体EF-ABCD中，四边形ADEF是正方形，FA⊥平面ABCD，BC∥AD，CD=l，AD=2| 2 |
①证明：CD⊥平面ABF；
②求二面角B-EF-A的正切值．
分析：①过点B作BC∥CD，交AD于点G，可证CD⊥AB，CD⊥FA，利用线面垂直的判定定理，可得CD⊥平面ABF；
②取EF的中点N，连接GN，则GN⊥EF，过点N作NM⊥EF，交BC于M，则∠GNM为二面角B-EF-A的平面角，由此可求二面角B-EF-A的正切值．
②取EF的中点N，连接GN，则GN⊥EF，过点N作NM⊥EF，交BC于M，则∠GNM为二面角B-EF-A的平面角，由此可求二面角B-EF-A的正切值．
解答：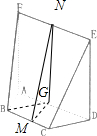
①证明：过点B作BC∥CD，交AD于点G，则∠BGA=∠CDA=45°，
由∠BAD=45°，可得BG⊥AB，从而CD⊥AB，
又FA⊥平面ABCD，∴CD⊥FA，
∵FA∩AB=A，∴CD⊥平面ABF．
②解：由上可得AG=
，即G为AD的中点，
取EF的中点N，连接GN，则GN⊥EF，
因为BC∥AD，所以BC∥EF，
过点N作NM⊥EF，交BC于M，则∠GNM为二面角B-EF-A的平面角，
连接GM，可得AD⊥平面GNM，故AD⊥GM，从而BC⊥GM，
由已知，可得GM=
，
由NG∥FA，FA⊥GM，得NG⊥GM，
在Rt△NGM中，tan∠GNM=
=
，
所以二面角B-EF-A的正切值为
．
①证明：过点B作BC∥CD，交AD于点G，则∠BGA=∠CDA=45°，由∠BAD=45°，可得BG⊥AB，从而CD⊥AB，
又FA⊥平面ABCD，∴CD⊥FA，
∵FA∩AB=A，∴CD⊥平面ABF．
②解：由上可得AG=
| 2 |
取EF的中点N，连接GN，则GN⊥EF，
因为BC∥AD，所以BC∥EF，
过点N作NM⊥EF，交BC于M，则∠GNM为二面角B-EF-A的平面角，
连接GM，可得AD⊥平面GNM，故AD⊥GM，从而BC⊥GM，
由已知，可得GM=
| ||
| 2 |
由NG∥FA，FA⊥GM，得NG⊥GM，
在Rt△NGM中，tan∠GNM=
| GM |
| NG |
| 1 |
| 4 |
所以二面角B-EF-A的正切值为
| 1 |
| 4 |
点评：本题考查线面垂直，考查面面角，考查学生分析解决问题的能力，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目