题目内容
已知函数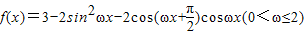 的图象过点
的图象过点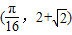 .
.(Ⅰ)求ω的值及使f(x)取得最小值的x的集合;
(Ⅱ)该函数的图象可由函数
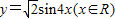 的图象经过怎样的变换得出?
的图象经过怎样的变换得出?
【答案】分析:(Ⅰ)由倍角公式和两角和的正弦公式对解析式进行化简,把已知点代入根据ω的范围求出ω的值,根据正弦函数的最小值,即当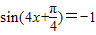 时,函数有最小值,求出对应的x的集合;
时,函数有最小值,求出对应的x的集合;
(Ⅱ)由(Ⅰ)求出的解析式和图象变换法则,即“左加右减”和“上加下减”,进行图象变换.
解答:解:(Ⅰ)f(x)=3-(1-cos2ωx)+2sinωcosωx=2+cos2ωx+sin2ωx(2分)
=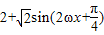 (3分)
(3分)
∵函数f(x)的图象过点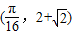
∴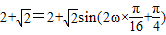
即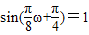 ,∴
,∴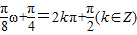
∴0<ω≤2,∴当k=0时,ω=2即的求ω的值为2(6分)
故
当f(x)取最小值时,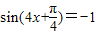 ,此时
,此时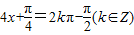
∴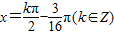 .
.
即,使f(x)取得最小值的x的集合为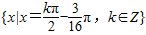 (9分)
(9分)
(Ⅱ)由(Ⅰ)可知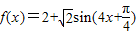
∴函数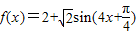 的图象可由
的图象可由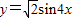 的图象经过以下变换得出;
的图象经过以下变换得出;
先把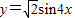 图象上所有的点向左平移
图象上所有的点向左平移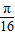 个单位长度,
个单位长度,
得到函数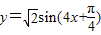 的图象,再把所得图象上的所有点,
的图象,再把所得图象上的所有点,
向上平移2个单位长度,从而得到函数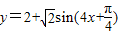 ,x∈R的图象.(12分)
,x∈R的图象.(12分)
点评:本题的考点是图象的变换和解析式的求法,应先对解析式化简再把条件代入,利用知识点有倍角公式和两角和的正弦公式,图象变换法则和正弦函数的性质,考查了整体思想.
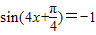 时,函数有最小值,求出对应的x的集合;
时,函数有最小值,求出对应的x的集合;(Ⅱ)由(Ⅰ)求出的解析式和图象变换法则,即“左加右减”和“上加下减”,进行图象变换.
解答:解:(Ⅰ)f(x)=3-(1-cos2ωx)+2sinωcosωx=2+cos2ωx+sin2ωx(2分)
=
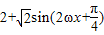 (3分)
(3分)∵函数f(x)的图象过点
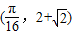
∴
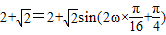
即
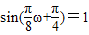 ,∴
,∴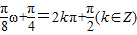
∴0<ω≤2,∴当k=0时,ω=2即的求ω的值为2(6分)
故

当f(x)取最小值时,
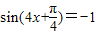 ,此时
,此时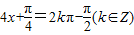
∴
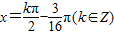 .
.即,使f(x)取得最小值的x的集合为
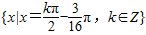 (9分)
(9分)(Ⅱ)由(Ⅰ)可知
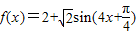
∴函数
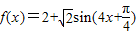 的图象可由
的图象可由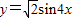 的图象经过以下变换得出;
的图象经过以下变换得出;先把
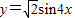 图象上所有的点向左平移
图象上所有的点向左平移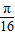 个单位长度,
个单位长度,得到函数
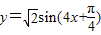 的图象,再把所得图象上的所有点,
的图象,再把所得图象上的所有点,向上平移2个单位长度,从而得到函数
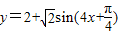 ,x∈R的图象.(12分)
,x∈R的图象.(12分)点评:本题的考点是图象的变换和解析式的求法,应先对解析式化简再把条件代入,利用知识点有倍角公式和两角和的正弦公式,图象变换法则和正弦函数的性质,考查了整体思想.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
 的图象过点A(3,7),则此函的最小值是 .
的图象过点A(3,7),则此函的最小值是 . 的图象过点
的图象过点 ,且图象上与点P最近的一个最低点是
,且图象上与点P最近的一个最低点是 .
. 的解析式;
的解析式; ,且
,且 为第三象限的角,求
为第三象限的角,求 的值;
的值; 在区间
在区间 上有零点,求
上有零点,求 的取值范围.
的取值范围. 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为 .
. 的解析式; (2)求函数
的解析式; (2)求函数