Question

（I）已知函数f(x)=

1-x

+

x+3

-1，求函数的定义域；
（II）画出函数f(x)=x+

|x|

x

的图象．

Answer 1

分析：（I）根据偶次根式有意义，根号下大于等于0建立关系，即可求出函数的定义域；
（II）讨论x的正负，去掉绝对值，得到分段函数，然后分段画出函数的图象即可．

解答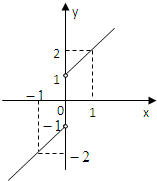：解：（I）要使原函数有意义，必须且只需

1-x≥0 x+3≥0

?-3≤x≤1，
所以原函数的定义域为[-3，1]．
（II）函数f(x)=x+

|x|

x

=

x+1  (x＞0) x-1 (x＜0)

，
其图象如图所示

点评：本题主要考查了函数的定义域、函数的图象，以及函数绝对值函数的处理方法，属于中档题．