题目内容
已知函数f(x)=|x-a|.
(Ⅰ)若不等式f(x)≥3的解集为{x|x≤1或x≥5},求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,若f(x)+f(x+4)≥m对一切实数x恒成立,求实数m的取值范围.
(Ⅰ)由f(x)≥3得|x-a|≥3,解得x≤a-3或x≥a+3.
又已知不等式f(x)≥3的解集为{x|x≤-1或x≥5},所以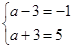 ,解得a=2.……5分
,解得a=2.……5分
(Ⅱ)当a=2时,f(x)=|x-2|,设g(x)=f(x)+f(x+4),
于是g(x)=|x-2|+|x+2|=[JB({]-2x,x<-24,-2≤x≤22x,x>2[JB)] 所以当x<-2时,g(x)>4;当-2≤x≤2时,g(x)=4;当x>2时,g(x)>4。
综上可得,g(x)的最小值为4.
从而若f(x)+f(x+4)≥m,即g(x)≥m对一切实数x恒成立,则m的取值范围为(-∞,4].
法二:(Ⅰ)同法一.
(Ⅱ)当a=2时,f(x)=|x-2|.设g(x)=f(x)+f(x+4).
由|x-2|+|x+2|≥|(x-2)-(x+2)|=4(当且仅当-2≤x≤2时等号成立),得g(x)的最小值为4.从而,若f(x)+f(x+4)≥m,即g(x)≥m对一切实数x恒成立.则m的取值范围为(-∞,4]?
解析

练习册系列答案
相关题目
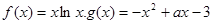
 在
在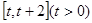 上的最小值;
上的最小值;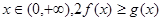 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.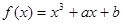 的图象是曲线C,直线
的图象是曲线C,直线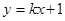 与曲线
与曲线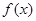 的解析式;
的解析式;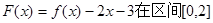 上的最大值和最小值.
上的最大值和最小值.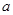 的正方形铁片,铁片的四角截去四个边长为
的正方形铁片,铁片的四角截去四个边长为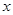 的小正方形,然后做成一个无盖方盒。
的小正方形,然后做成一个无盖方盒。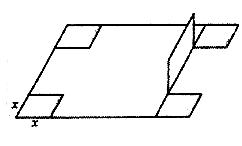
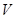 表示成
表示成 ≥10)层,则每平方米的平均建筑费用为560+48
≥10)层,则每平方米的平均建筑费用为560+48 )
) 万件与促销费用
万件与促销费用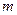 万元(
万元(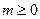 )满足
)满足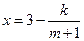 (
(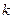 为常数),如果不搞促销活动,则该产品的年销量只能是1万件。已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品的年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)。
为常数),如果不搞促销活动,则该产品的年销量只能是1万件。已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品的年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)。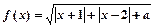 .
.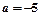 时,求函数
时,求函数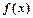 的定义域;
的定义域;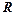 ,试求
,试求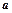 的取值范围
的取值范围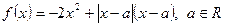 。
。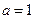 时,解不等式
时,解不等式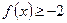 ;
;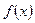 的最大值。
的最大值。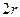 ,短半轴长为
,短半轴长为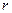 ,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记
,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记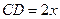 ,梯形面积为S.
,梯形面积为S. 求面积S以
求面积S以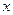 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;