Question

【题目】如图所示，建立空间直角坐标系Dxyz，已知正方体ABCD﹣A1B1C1D1的棱长为1，点M是正方体对角线D1B的中点，点N在棱CC1上．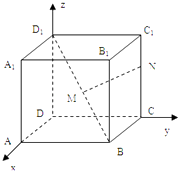

（1）当2|C1N|=|NC|时，求|MN|；
（2）当点N在棱CC1上移动时，求|MN|的最小值并求此时的N点坐标．

Answer 1

【答案】
（1）解：∵如图所示，建立空间直角坐标系Dxyz，

正方体ABCD﹣A1B1C1D1的棱长为1，点M是正方体对角线D1B的中点，

点N在棱CC1上，2|C1N|=|NC|，

∴D1（0，0，1），B（1，1，0），M（ ），N（0，1， ），

∴|MN|= =

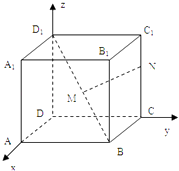
（2）解：∵点M是正方体对角线D1B的中点，点N在棱CC1上移动时，

∴当MN是BD1和CC1的公垂线时，|MN|取最小值，

∴当N是CC1中点时，|MN|取最小值，

此时N（0，1， ），|MN|min= =

【解析】（1）求出M（ ），N（0，1， ），由此能求出|MN|．（2）当MN是BD1和CC1的公垂线时，|MN|取最小值，由此得到当N是CC1中点时，|MN|取最小值．