题目内容
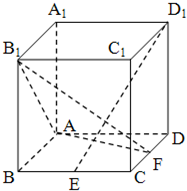 如图,正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F 是棱CD上的动点.
如图,正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F 是棱CD上的动点.(Ⅰ)试确定点F的位置,使得D1E⊥平面AB1F;
(Ⅱ)当D1E⊥平面AB1F时,求二面角C1-EF-A的余弦值以及BA1与面C1EF所成的角的大小.
分析:(1)建立空间直角坐标系,写出要用的点的坐标,再设出点F的坐标,利用线面垂直得到直线所在的向量与平面内的任何一个向量的数量积等于0,求出F点的坐标,进而能够确定F的位置.
(2)根据正方体的结构特征首先看出平面的一个法向量,再设出另一个平面的法向量,根据法向量与平面上的向量数量积等于0,求另一个平面的一个法向量,再根据两个向量的有关运算求出两个向量的夹角,进而转化为二面角的平面角的余弦值求出答案即可.而线面角的求法是:首先计算出斜线所在的向量与平面的法向量的夹角,再根据此角与线面角的关系得到线面角.
(2)根据正方体的结构特征首先看出平面的一个法向量,再设出另一个平面的法向量,根据法向量与平面上的向量数量积等于0,求另一个平面的一个法向量,再根据两个向量的有关运算求出两个向量的夹角,进而转化为二面角的平面角的余弦值求出答案即可.而线面角的求法是:首先计算出斜线所在的向量与平面的法向量的夹角,再根据此角与线面角的关系得到线面角.
解答:解:(I)由题意可得:以A为原点,分别以直线AB、AD、AA1为x轴、y轴、z轴建立空间直角坐标系,不妨设正方体的棱长为1,且DF=x,则A1(0,0,1),A(0,0,0),B(1,0,0),D(0,1,0),B1(1,0,1),D1(0,1,1),E(1,
,0),F(x,1,0)
所以
=(1,-
,-1),
=(1,0,1),
=(x,1,0)
由D1E⊥面AB1F?
⊥
且
⊥
,
所以
,可解得x=
所以当点F是CD的中点时,D1E⊥平面AB1F.
(II)当D1E⊥平面AB1F时,F是CD的中点,F(
,1,0)
由正方体的结构特征可得:平面AEF的一个法向量为
=(0,0,1),
设平面C1EF的一个法向量为
=(x,y,z),
在平面C1EF中,
=(0,
,1),
=(-
,
,0),
所以
,即
,
所以取平面C1EF的一个法向量为
=(2,2,-1),
所以cos<
,
>=-
,
所以<
,
>=π-arccos
,
又因为当把
,
都移向这个二面角内一点时,
背向平面AEF,而
指向平面C1EF,
所以二面角C1-EF-A的大小为π-arccos
又因为
=(-1,0,1),
所以cos<
,
>=-
,
所以<
,
>=135?,
∴BA1与平面C1EF所成的角的大小为45°.
| 1 |
| 2 |
所以
| D1E |
| 1 |
| 2 |
| AB1 |
| AF |
由D1E⊥面AB1F?
| D1E |
| AB1 |
| D1E |
| AF |
所以
|
| 1 |
| 2 |
所以当点F是CD的中点时,D1E⊥平面AB1F.
(II)当D1E⊥平面AB1F时,F是CD的中点,F(
| 1 |
| 2 |
由正方体的结构特征可得:平面AEF的一个法向量为
| m |
设平面C1EF的一个法向量为
| n |
在平面C1EF中,
| EC1 |
| 1 |
| 2 |
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
所以
|
|
所以取平面C1EF的一个法向量为
| n |
所以cos<
| m |
| n |
| 1 |
| 3 |
所以<
| m |
| n |
| 1 |
| 3 |
又因为当把
| m |
| n |
| m |
| n |
所以二面角C1-EF-A的大小为π-arccos
| 1 |
| 3 |
又因为
| BA1 |
所以cos<
| BA1 |
| n |
| ||
| 2 |
所以<
| BA1 |
| n |
∴BA1与平面C1EF所成的角的大小为45°.
点评:解决此类问题的关键是熟练掌握利用空间向量判定线面垂直与利用空间向量求空间角的方法,求二面角的平面角与线面的关键是正确求出平面的法向量,再利用向量之间的有关运算求出向量的夹角,进而把向量的夹角转化为空间角.区分二面角与面面角是易错点,本题较好的处理了这一点,利用法向量的指向确定出二面角是钝角,此方法值得借鉴推广

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量
如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量 如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.
如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG. 如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( )
如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( ) 如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且
如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且