题目内容
已知函数f(x)=ax2+(1-3a)x+a在区间[1,+∞)上递增,求a的取值范围是________.
0≤a≤1
分析:由已知中函数f(x)=ax2+(1-3a)x+a在区间[1,+∞)上递增,结合一次函数和二次函数的图象和性质,分别讨论a=0时和a≠0时,满足条件的a的取值范围,综合后,即可得到a的取值范围.
解答:若a=0,则函数f(x)=ax2+(1-3a)x+a=x,
此时函数f(x)在区间[1,+∞)上递增,满足条件;
若a≠0,若函数f(x)=ax2+(1-3a)x+a在区间[1,+∞)上递增,
则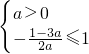
解得:0<a≤1
综上,a的取值范围是0≤a≤1
故答案为0≤a≤1
点评:本题考查的知识点是二次函数的性质,其中熟练掌握一次函数和二次函数的单调性是解答本题的关键.解答中易忽略a=0,则函数f(x)=x也满足题目要求,而错解为0<a≤1.
分析:由已知中函数f(x)=ax2+(1-3a)x+a在区间[1,+∞)上递增,结合一次函数和二次函数的图象和性质,分别讨论a=0时和a≠0时,满足条件的a的取值范围,综合后,即可得到a的取值范围.
解答:若a=0,则函数f(x)=ax2+(1-3a)x+a=x,
此时函数f(x)在区间[1,+∞)上递增,满足条件;
若a≠0,若函数f(x)=ax2+(1-3a)x+a在区间[1,+∞)上递增,
则
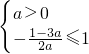
解得:0<a≤1
综上,a的取值范围是0≤a≤1
故答案为0≤a≤1
点评:本题考查的知识点是二次函数的性质,其中熟练掌握一次函数和二次函数的单调性是解答本题的关键.解答中易忽略a=0,则函数f(x)=x也满足题目要求,而错解为0<a≤1.

练习册系列答案
相关题目