Question

【题目】已知在几何体ABCDE中，AB⊥平面BCE，且△BCE是正三角形，四边形ABCD为正方形，F是线段CD上的中点，G是线段BE的中点，且AB=2．

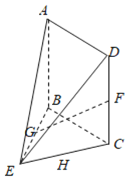
（1）求证：GF∥平面ADE；

（2）求三棱锥F–BGC的表面积．

Answer 1

【答案】（1）证明见解析（2）

【解析】

（1）取AB中点H，连结HF，GH，推导出平面HGF∥平面ADE，由此能证明GF∥平面ADE；（2）推导出CF⊥BC，CF⊥CG，CG⊥BG，CF=1，BC=2，BG=1，，三棱锥的表面积：．

（1）取AB中点H，连结HF，GH，

∵F是线段CD上的中点，G是线段BE的中点，

∴HF∥AD，GH∥AE，

∵HF∩HG=H，AD∩AE=A，HF、HG平面HGF，AD、AE平面ADE，

∴平面HGF∥平面ADE，

∵GF平面HGF，

∴GF∥平面ADE．

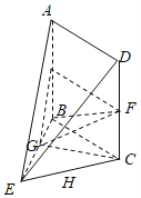
（2）∵在几何体ABCDE中，AB⊥平面BCE，

且△BCE是正三角形，四边形ABCD为正方形，

F是线段CD上的中点，G是线段BE的中点，且AB=2．

∴CF⊥BC，CF⊥CG，CG⊥BG，CF=1，BC=2，BG=1，，

∴三棱锥F–BGC的表面积：

.