题目内容
设命题P:函数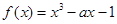 在区间[-1,1]上单调递减;
在区间[-1,1]上单调递减;
命题q:函数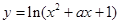 的值域是R.如果命题p或q为真命题,p且q为假命题,求
的值域是R.如果命题p或q为真命题,p且q为假命题,求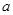 的取值范围.
的取值范围.
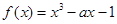 在区间[-1,1]上单调递减;
在区间[-1,1]上单调递减;命题q:函数
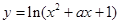 的值域是R.如果命题p或q为真命题,p且q为假命题,求
的值域是R.如果命题p或q为真命题,p且q为假命题,求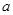 的取值范围.
的取值范围.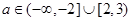
试题分析:由函数
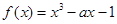 在区间[-1,1]上单调递减转化为其导函数
在区间[-1,1]上单调递减转化为其导函数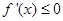 在[-1,1]上恒成立,分离变量可求解;由函数
在[-1,1]上恒成立,分离变量可求解;由函数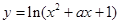 的值域是R转化为
的值域是R转化为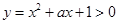 对任意的实数
对任意的实数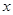 有意义,因此其判别式
有意义,因此其判别式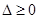 .再结合两命题的真假分类讨论求解
.再结合两命题的真假分类讨论求解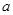 的取值范围.
的取值范围.试题解析:p为真命题
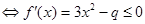 在
在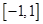 上恒成立,
上恒成立,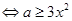 在
在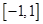 上恒成立
上恒成立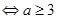 4分
4分q为真命题
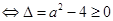 恒成立
恒成立 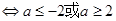 6分
6分由题意p和q有且只有一个是真命题
P真q假
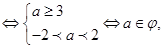 p假q真
p假q真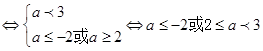
综上所述:
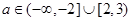 . 12分
. 12分
练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
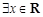 ,使得
,使得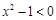 的否定是:
的否定是: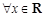 ,均有
,均有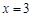 ,则
,则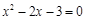 的否命题是:若
的否命题是:若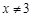 ,则
,则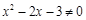 .
.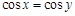 ,则
,则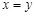 的逆否命题是真命题.
的逆否命题是真命题.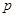 :
: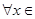 [0,l],
[0,l],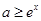 ,命题
,命题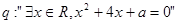 若命题“
若命题“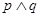 ”是真命题,则实数
”是真命题,则实数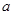 的取值范围是 .
的取值范围是 .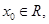 使得
使得
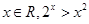
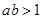 ,则
,则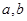 至少有一个大于1
至少有一个大于1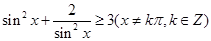
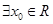 ,x0≤1或
,x0≤1或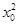 >4”的否定是________.
>4”的否定是________.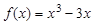 ,并设:
,并设: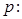
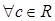 ,
,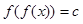 至少有3个实根;
至少有3个实根;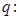 当
当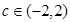 时,方程
时,方程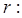 当
当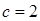 时,方程
时,方程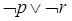
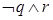
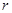
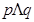
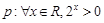 ,那么命题
,那么命题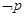 为( )
为( )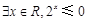
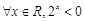
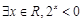
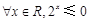
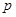 :“
:“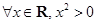 ”,则( )
”,则( )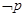 :
: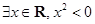
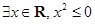

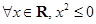
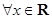 ,
,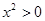 ”的否定是
”的否定是