题目内容
(本小题满分12分)
已知函数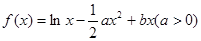 且导数
且导数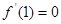 .
.
(1)试用含有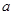 的式子表示
的式子表示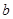 ,并求
,并求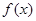 的单调区间;
的单调区间;
(2)对于函数图象上不同的两点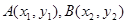 ,且
,且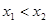 ,如果在函数图像上存在点
,如果在函数图像上存在点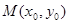 (其中
(其中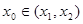 )使得点
)使得点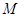 处的切线
处的切线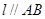 ,则称
,则称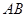 存在“相依切线”.特别地,当
存在“相依切线”.特别地,当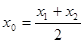 时,又称
时,又称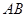 存在“中值相依切线”.试问:在函数
存在“中值相依切线”.试问:在函数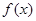 上是否存在两点
上是否存在两点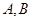 使得它存在“中值相依切线”?若存在,求
使得它存在“中值相依切线”?若存在,求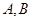 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】
(1) 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 ;
;
(2)不存在点 满足题意.
满足题意.
【解析】(1)求导,根据 ,可得
,可得 ,然后根据
,然后根据 可得
可得
 。
。 函数
函数 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为
(2)解本题的突破口是假设存在点 满足条件,
满足条件,
则 ,整理得:
,整理得: ,
,
令 ,则问题转化为方程:
,则问题转化为方程: 有根.
有根.
然后构造函数 求导解决。
求导解决。
解:(1) ,
, ,
, ,
…………… 1分
,
…………… 1分  ,
, (舍去),
(舍去), ,……… 2分
,……… 2分  函数
函数 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 .……………… 4分
.……………… 4分
(2) 假设存在点 满足条件,
满足条件,
则 ,整理得:
,整理得: ,
……………… 6分
,
……………… 6分
令 ,则问题转化为方程:
,则问题转化为方程: 有根,
有根,
设 ,
, ,……………… 9分
,……………… 9分
 函数
函数 为
为 上的单调递增函数,且
上的单调递增函数,且 ,
, ,
,
所以不存在 使方程
使方程 成立,
成立,
即不存在点 满足题意.
……………… 12分
满足题意.
……………… 12分

练习册系列答案
相关题目