题目内容
求满足下列条件的曲线方程:
(1)经过两点P(-2
,1),Q(
,-2)的椭圆的标准方程;
(2)与双曲线
-
=1有公共渐近线,且经过点(-3,2
)的双曲线的标准方程;
(3)焦点在直线x+3y+15=0上的抛物线的标准方程.
(1)经过两点P(-2
| 3 |
| 3 |
(2)与双曲线
| x2 |
| 9 |
| y2 |
| 16 |
| 3 |
(3)焦点在直线x+3y+15=0上的抛物线的标准方程.
分析:(1)设出椭圆方程,代入点的坐标,建立方程组,即可求得椭圆的标准方程.
(2)据共渐近线的双曲线的方程的一般形式设出双曲线的方程,将点的坐标代入求出待定系数λ,即得到要求的双曲线方程.
(3)分焦点在x轴和y轴两种情况分别求出焦点坐标,然后根据抛物线的标准形式可得答案.
(2)据共渐近线的双曲线的方程的一般形式设出双曲线的方程,将点的坐标代入求出待定系数λ,即得到要求的双曲线方程.
(3)分焦点在x轴和y轴两种情况分别求出焦点坐标,然后根据抛物线的标准形式可得答案.
解答:解:(1)依题意,可设椭圆的方程为
+
=1(m>0,n>0),则
∴椭圆经过两点P(-2
,1),Q(
,-2),
∴
+
=1且
+
=1
∴m=15,n=5
∴经过两点P(-2
,1),Q(
,-2)的椭圆的标准方程为
+
=1;
(2)设所求双曲线的方程为
-
=λ(λ≠0),
将点(-3,2
)代入得λ=
,
所求双曲线的标准方程为
-
=1;
(3)令x=0得y=-5;令y=0得x=-15;
∴抛物线的焦点坐标为:(-15,0),(0,-5)
当焦点为(-15,0)时,即
=15,
∴p=30,此时抛物线方程为:y2=-60x:
当焦点为(0,-5)时,即
=5,
∴p=10,此时抛物线方程为:x2=-20y;
故所求抛物线的标准方程为:y2=-60x 或x2=-20y.
| x2 |
| m |
| y2 |
| n |
∴椭圆经过两点P(-2
| 3 |
| 3 |
∴
| 12 |
| m |
| 1 |
| n |
| 3 |
| m |
| 4 |
| n |
∴m=15,n=5
∴经过两点P(-2
| 3 |
| 3 |
| x2 |
| 15 |
| y2 |
| 5 |
(2)设所求双曲线的方程为
| x2 |
| 9 |
| y2 |
| 16 |
将点(-3,2
| 3 |
| 1 |
| 4 |
所求双曲线的标准方程为
| 4x2 |
| 9 |
| y2 |
| 4 |
(3)令x=0得y=-5;令y=0得x=-15;
∴抛物线的焦点坐标为:(-15,0),(0,-5)
当焦点为(-15,0)时,即
| p |
| 2 |
∴p=30,此时抛物线方程为:y2=-60x:
当焦点为(0,-5)时,即
| p |
| 2 |
∴p=10,此时抛物线方程为:x2=-20y;
故所求抛物线的标准方程为:y2=-60x 或x2=-20y.
点评:本题考查圆锥曲线的标准方程和简单性质,考查学生的计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
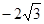 ,1),Q(
,1),Q(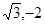 )的椭圆的标准方程.
)的椭圆的标准方程.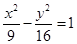 有共同的渐近线,且经过点
有共同的渐近线,且经过点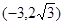 的双曲线的标准方程.
的双曲线的标准方程.