题目内容
求满足下列条件的曲线的标准方程:
(1)对称轴是x轴,并且顶点到焦点的距离等于8的抛物线;
(2)a=10,e=
,焦点在x轴上的椭圆;
(3)到点(0,-10),(0,10)距离之差的绝对值为16的双曲线.
(1)对称轴是x轴,并且顶点到焦点的距离等于8的抛物线;
(2)a=10,e=
| 3 | 5 |
(3)到点(0,-10),(0,10)距离之差的绝对值为16的双曲线.
分析:(1)由已知条件,设出抛物线的标准方程,求出p,由此能求出抛物线方程;
(2)由已知条件,设出椭圆的标准方程,由已知条件分别求出a,b,由此能求出椭圆方程;
(3)利用双曲线的定义,根据已知条件能求出双曲线的方程.
(2)由已知条件,设出椭圆的标准方程,由已知条件分别求出a,b,由此能求出椭圆方程;
(3)利用双曲线的定义,根据已知条件能求出双曲线的方程.
解答:解:(1)∵抛物线的对称轴是x轴,
∴设抛物线方程为y2=2px,p>0,或y2=-2px,p>0,
∴抛物线的顶点到焦点的距离等于8,
∴
=8,解得p=16,
∴抛物线方程为y2=32x,或y2=-32x.
(2)∵椭圆焦点在x轴上,
∴设椭圆方程为
+
=1,
∵a=10,e=
,
∴c=6,b2=102-62=64,
∴椭圆方程为
+
=1.
(3)∵双曲线上的点到点(0,-10),(0,10)距离之差的绝对值为16,
∴双曲线的焦点在y轴上,且c=10,2a=16,
∴b2=102-(
)2=36,
∴双曲线方程为
-
=1.
∴设抛物线方程为y2=2px,p>0,或y2=-2px,p>0,
∴抛物线的顶点到焦点的距离等于8,
∴
| p |
| 2 |
∴抛物线方程为y2=32x,或y2=-32x.
(2)∵椭圆焦点在x轴上,
∴设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
∵a=10,e=
| 3 |
| 5 |
∴c=6,b2=102-62=64,
∴椭圆方程为
| x2 |
| 100 |
| y2 |
| 64 |
(3)∵双曲线上的点到点(0,-10),(0,10)距离之差的绝对值为16,
∴双曲线的焦点在y轴上,且c=10,2a=16,
∴b2=102-(
| 16 |
| 2 |
∴双曲线方程为
| y2 |
| 64 |
| x2 |
| 36 |
点评:本题考查抛物线、椭圆、双曲线的性质及其应用,解题时要认真审题,熟练掌握抛物线、椭圆、双曲线的基础知识.

练习册系列答案
相关题目
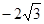 ,1),Q(
,1),Q(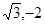 )的椭圆的标准方程.
)的椭圆的标准方程.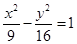 有共同的渐近线,且经过点
有共同的渐近线,且经过点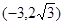 的双曲线的标准方程.
的双曲线的标准方程.