题目内容
设α为常数,求证:y=f(x)=cos2x+cos2(x+α)-2cosαcosxcos(x+α).表示平行于x轴的直线(α≠kπ,k∈Z).
分析:要想证明y=f(x)=cos2x+cos2(x+α)-2cosαcosxcos(x+α).表示平行于x轴的直线(α≠kπ,k∈Z).且又有设α为常数,则证明的方向是将函数的解析式进行化简,化简成一个不含x的常数.
解答:证明:y=f(x)=cos2x+cos2(x+α)-2cosαcosxcos(x+α)
=cos2x+cos2(x+α)-2cosxcos(x+α)cos[(x+α)-x]
=cos2x+cos2(x+α)-2cosxcos(x+α)[cos(x+α)cosx+sin(x+α)sinx]
=cos2x+cos2(x+α)-2cosxcos(x+α)cos(x+α)cosx-2cosxcos(x+α)sin(x+α)sinx
=cos2x+cos2(x+α)-2cos2xcos2(x+α)-2cosxcos(x+α)sin(x+α)sinx
=[cos2x-cos2xcos2(x+α)]+[cos2(x+α)-cos2xcos2(x+α)]-2cosxcos(x+α)sin(x+α)sinx
=cos2xsin2(x+α)+cos2(x+α)sin2x-2cosxcos(x+α)sin(x+α)sinx
=[cosxsin(x+α)-cos(x+α)sinx]2
=sin2[(x+α)-x]=sin2α
又∵α为常数
∴y=f(x)表示平行于x轴的直线
=cos2x+cos2(x+α)-2cosxcos(x+α)cos[(x+α)-x]
=cos2x+cos2(x+α)-2cosxcos(x+α)[cos(x+α)cosx+sin(x+α)sinx]
=cos2x+cos2(x+α)-2cosxcos(x+α)cos(x+α)cosx-2cosxcos(x+α)sin(x+α)sinx
=cos2x+cos2(x+α)-2cos2xcos2(x+α)-2cosxcos(x+α)sin(x+α)sinx
=[cos2x-cos2xcos2(x+α)]+[cos2(x+α)-cos2xcos2(x+α)]-2cosxcos(x+α)sin(x+α)sinx
=cos2xsin2(x+α)+cos2(x+α)sin2x-2cosxcos(x+α)sin(x+α)sinx
=[cosxsin(x+α)-cos(x+α)sinx]2
=sin2[(x+α)-x]=sin2α
又∵α为常数
∴y=f(x)表示平行于x轴的直线
点评:本题的证明过程比较复杂,为了得到证明方向,我们可以先代入特殊值,如x=0,先来判断结果是一个什么样的常数,再逆推一下寻找解题的思路.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
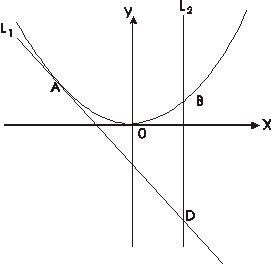 已知点A(-1,2)是抛物线C:y=2x2上的点,直线l1过点A,且与抛物线C相切,直线l2:x=a(a≠-1)交抛物线C于点B,交直线l1于点D.
已知点A(-1,2)是抛物线C:y=2x2上的点,直线l1过点A,且与抛物线C相切,直线l2:x=a(a≠-1)交抛物线C于点B,交直线l1于点D.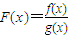 ,若函数F(x)在区间(0,1]上是单调函数,求a的取值范围.
,若函数F(x)在区间(0,1]上是单调函数,求a的取值范围. ,若函数F(x)在区间(0,1]上是单调函数,求a的取值范围.
,若函数F(x)在区间(0,1]上是单调函数,求a的取值范围.