题目内容
已知a为常数,a∈R,函数f(x)=x2+ax-lnx,g(x)=ex.(其中e是自然对数的底数)(Ⅰ)过坐标原点O作曲线y=f(x)的切线,设切点为P(x,y),求证:x=1;
(Ⅱ)令
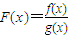 ,若函数F(x)在区间(0,1]上是单调函数,求a的取值范围.
,若函数F(x)在区间(0,1]上是单调函数,求a的取值范围.
【答案】分析:(I)先对函数求导,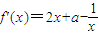 ,可得切线的斜率
,可得切线的斜率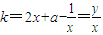 =
=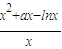
,即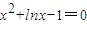 ,由x=1是方程的解,且y=x2+lnx-1在(0,+∞)上是增函数,可证
,由x=1是方程的解,且y=x2+lnx-1在(0,+∞)上是增函数,可证
(Ⅱ)由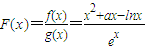 ,
,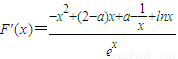 ,先研究函数
,先研究函数 ,则
,则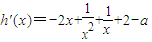 .
.
由h'(x)在(0,1]上是减函数,可得h'(x)≥h'(1)=2-a,通过研究2-a的正负可判断h(x)的单调性,进而可得函数F(x)的单调性,可求
解答:解:(I)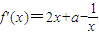 (x>0). …(2分)
(x>0). …(2分)
过切点P(x,y)的切线的斜率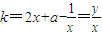 =
=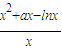
整理得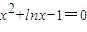 .…(4分)
.…(4分)
显然,x=1是这个方程的解,又因为y=x2+lnx-1在(0,+∞)上是增函数,
所以方程x2+lnx-1=0有唯一实数解.故x=1.…(6分)
(Ⅱ)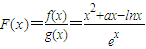 ,
,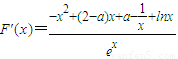 .…(8分)
.…(8分)
设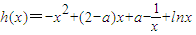 ,则
,则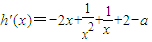 .
.
易知h'(x)在(0,1]上是减函数,从而h'(x)≥h'(1)=2-a. …(10分)
(1)当2-a≥0,即a≤2时,h'(x)≥0,h(x)在区间(0,1)上是增函数.
∵h(1)=0,∴h(x)≤0在(0,1]上恒成立,即F'(x)≤0在(0,1]上恒成立.
∴F(x)在区间(0,1]上是减函数.
所以,a≤2满足题意. …(12分)
(2)当2-a<0,即a>2时,设函数h'(x)的唯一零点为x,
则h(x)在(0,x)上递增,在(x,1)上递减.又∵h(1)=0,∴h(x)>0.
又∵h(e-a)=-e-2a+(2-a)e-a+a-ea+lne-a<0,
∴h(x)在(0,1)内有唯一一个零点x',
当x∈(0,x')时,h(x)<0,当x∈(x',1)时,h(x)>0.
从而F(x)在(0,x')递减,在(x',1)递增,与在区间(0,1]上是单调函数矛盾.
∴a>2不合题意.
综合(1)(2)得,a≤2. …(15分)
点评:考查学生利用导数研究函数的单调能力,函数单调性的判定,以及导数的运算,试题具有一定的综合性.
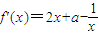 ,可得切线的斜率
,可得切线的斜率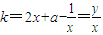 =
=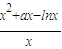
,即
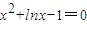 ,由x=1是方程的解,且y=x2+lnx-1在(0,+∞)上是增函数,可证
,由x=1是方程的解,且y=x2+lnx-1在(0,+∞)上是增函数,可证(Ⅱ)由
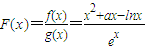 ,
,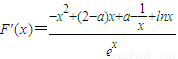 ,先研究函数
,先研究函数 ,则
,则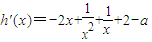 .
.由h'(x)在(0,1]上是减函数,可得h'(x)≥h'(1)=2-a,通过研究2-a的正负可判断h(x)的单调性,进而可得函数F(x)的单调性,可求
解答:解:(I)
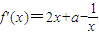 (x>0). …(2分)
(x>0). …(2分)过切点P(x,y)的切线的斜率
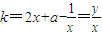 =
=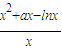
整理得
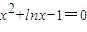 .…(4分)
.…(4分)显然,x=1是这个方程的解,又因为y=x2+lnx-1在(0,+∞)上是增函数,
所以方程x2+lnx-1=0有唯一实数解.故x=1.…(6分)
(Ⅱ)
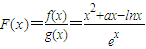 ,
,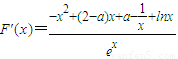 .…(8分)
.…(8分)设
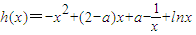 ,则
,则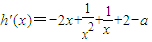 .
.易知h'(x)在(0,1]上是减函数,从而h'(x)≥h'(1)=2-a. …(10分)
(1)当2-a≥0,即a≤2时,h'(x)≥0,h(x)在区间(0,1)上是增函数.
∵h(1)=0,∴h(x)≤0在(0,1]上恒成立,即F'(x)≤0在(0,1]上恒成立.
∴F(x)在区间(0,1]上是减函数.
所以,a≤2满足题意. …(12分)
(2)当2-a<0,即a>2时,设函数h'(x)的唯一零点为x,
则h(x)在(0,x)上递增,在(x,1)上递减.又∵h(1)=0,∴h(x)>0.
又∵h(e-a)=-e-2a+(2-a)e-a+a-ea+lne-a<0,
∴h(x)在(0,1)内有唯一一个零点x',
当x∈(0,x')时,h(x)<0,当x∈(x',1)时,h(x)>0.
从而F(x)在(0,x')递减,在(x',1)递增,与在区间(0,1]上是单调函数矛盾.
∴a>2不合题意.
综合(1)(2)得,a≤2. …(15分)
点评:考查学生利用导数研究函数的单调能力,函数单调性的判定,以及导数的运算,试题具有一定的综合性.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
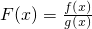 ,若函数F(x)在区间(0,1]上是单调函数,求a的取值范围.
,若函数F(x)在区间(0,1]上是单调函数,求a的取值范围. ,若函数F(x)在区间(0,1]上是单调函数,求a的取值范围.
,若函数F(x)在区间(0,1]上是单调函数,求a的取值范围.