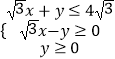题目内容
【题目】已知函数f(x)=  ,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )
,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )
A.(4,2018)
B.(4,2020)
C.(3,2020)
D.(2,2020)
【答案】B
【解析】解:作出函数的图象如图,直线y=m交函数图象于如图,

不妨设a<b<c,
由正弦曲线的对称性,可得(a,m)与(b,m)关于直线x=1对称,
因此a+b=2.
当直线y=m=1时,由log2017(x﹣1)=1,
解得x﹣1=2017,即x=2018,
∴若满足f(a)=f(b)=f(c),(a、b、c互不相等),
由a<b<c可得2<c<2018,
因此可得4<a+b+c<2020,
即a+b+c∈(4,2020),
故选:B

练习册系列答案
相关题目