题目内容
(2011•南汇区二模)在极坐标系中,曲线ρ=cosθ+sinθ关于极轴的对称曲线的极坐标方程为
ρ=cosθ-sinθ
ρ=cosθ-sinθ
.分析:利用直角坐标与极坐标间的关系:ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换求出直角坐标方程,然后求出关于x轴对称后的曲线方程,再将直角坐标方程画出极坐标方程.
解答:解:ρ=cosθ+sinθ两边同乘以ρ得
ρ2=ρcosθ+ρsinθ即x2+y2=x+y
关于x轴对称后的曲线方程为x2+y2=x-y
∴关于极轴的对称曲线的极坐标方程为ρ=cosθ-sinθ
故答案为:ρ=cosθ-sinθ
ρ2=ρcosθ+ρsinθ即x2+y2=x+y
关于x轴对称后的曲线方程为x2+y2=x-y
∴关于极轴的对称曲线的极坐标方程为ρ=cosθ-sinθ
故答案为:ρ=cosθ-sinθ
点评:本题主要考查了简单曲线的极坐标方程,以及极坐标方程与直角方程的互化和对称变换,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
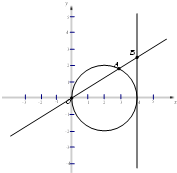 (2011•南汇区二模)已知动直线y=kx交圆(x-2)2+y2=4于坐标原点O和点A,交直线x=4于点B,若动点M满足
(2011•南汇区二模)已知动直线y=kx交圆(x-2)2+y2=4于坐标原点O和点A,交直线x=4于点B,若动点M满足