题目内容
【题目】已知对任意平面向量![]() ,把
,把![]() 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转![]() 角得到向量
角得到向量![]() ,
,![]() ,叫做把点
,叫做把点![]() 绕点
绕点![]() 逆时针方向旋转
逆时针方向旋转![]() 角得到点
角得到点![]() .
.
(1)已知平面内点![]() ,点
,点![]() ,把点
,把点![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 后得到点
后得到点![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设平面内曲线![]() 上的每一点绕坐标原点沿逆时针方向旋转
上的每一点绕坐标原点沿逆时针方向旋转![]() 后得到的点的轨迹方程是曲线
后得到的点的轨迹方程是曲线![]() ,求原来曲线
,求原来曲线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)求出向量![]() 的坐标表示,由点
的坐标表示,由点![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 后得到点
后得到点![]() ,相当于点
,相当于点![]() 绕点
绕点![]() 逆时针方向旋转
逆时针方向旋转![]() ,设出点
,设出点![]() 的坐标,写出向量
的坐标,写出向量![]() 的坐标,根据已知给的公式,得到一个二元一次方程组,解这个方程组,求出点
的坐标,根据已知给的公式,得到一个二元一次方程组,解这个方程组,求出点![]() 的坐标;
的坐标;
(2)设平面内曲线![]() 上的每一点
上的每一点![]() ,
,![]() 绕坐标原点沿逆时针方向旋转
绕坐标原点沿逆时针方向旋转![]() 后得到的点
后得到的点![]() ,根据已知条件给的公式,可以得到一个方程组,可以分别求出
,根据已知条件给的公式,可以得到一个方程组,可以分别求出![]() 与
与![]() 的关系,结合
的关系,结合![]() ,可以求出原来曲线
,可以求出原来曲线![]() 的方程.
的方程.
由已知可得:![]()
将点![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() ,即是点
,即是点![]() 绕点
绕点![]() 逆时针方向旋转
逆时针方向旋转![]() ,
,
即可得到点![]()
设点![]() ,则
,则![]()
所以![]()
![]()
所以![]() ,解得
,解得![]()
所以点![]() 的坐标为
的坐标为![]()
(2)设平面内曲线![]() 上的每一点
上的每一点![]() ,
,![]() 绕坐标原点沿逆时针方向旋转
绕坐标原点沿逆时针方向旋转![]() 后得到的点
后得到的点![]()
则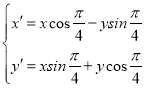 即
即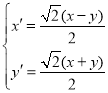
又![]() ,所以
,所以![]() ,即
,即![]()
所以曲线![]() 的方程为
的方程为![]()

练习册系列答案
相关题目

