题目内容
已知圆满足:①截y轴所得的弦长为2;②被x轴分成两段圆弧,其弧长的比为3∶1,在满足条件①②的所有圆中,求圆心到直线l:x-2y=0距离最小的圆的方程.
解析:方法一:设圆心C的坐标为(a,b),半径为r,由题设知圆C截x轴所得劣弧所对的圆心角为90°,圆C截x轴所得弦长为![]() r,所以r=
r,所以r=![]() |b|.?
|b|.?
又截y轴所得的弦长为2,所以r2=a2+1.所以2b2-a2=1.?
圆心C(a,b)到直线l:x-2y=0的距离![]() 即5d2=(a-2b)2=a2+4b2-4ab≥a2+4b2-2(a2+b2)=2b2-a2=1,当且仅当a=b时取等号,此时5d2=1,从而d取最小值.?
即5d2=(a-2b)2=a2+4b2-4ab≥a2+4b2-2(a2+b2)=2b2-a2=1,当且仅当a=b时取等号,此时5d2=1,从而d取最小值.?
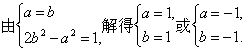
于是有r=![]() .
.
所求圆的方程为(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2.?
方法二:由方法一,得![]()
所以a-2b=±![]() d,a=2b±
d,a=2b±![]() d.
d.
代入2b2-a2=1,得2b2±4![]() bd+5d2+1=0.(*)?
bd+5d2+1=0.(*)?
将其视为关于b的一元二次方程,因为b∈R,?
所以Δ=8(5d2-1)≥0,即5d2≥1.?
从而d有最小值![]() .代入(*)式,?
.代入(*)式,?
解得b=±1,a=±1,余下同方法一.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 ,求圆的方程.
,求圆的方程. ,求该圆的方程.
,求该圆的方程.