题目内容
【题目】如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不垂直的是![]()
![]()
A. 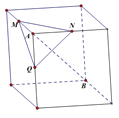 B.
B. 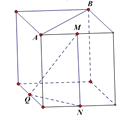
C. 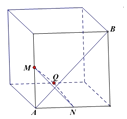 D.
D. 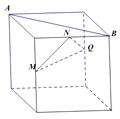
【答案】D
【解析】
由中位线定理和异面直线所成角,以及线面垂直的判定定理,即可得到正确结论.
解:对于A,AB为体对角线,MN,MQ,NQ分别为棱的中点,由中位线定理可得它们平行于所对应的面对角线,连接另一条面对角线,由线面垂直的判定可得AB垂直于MN,MQ,NQ,可得AB垂直于平面MNQ;
对于B,AB为上底面的对角线,显然AB垂直于MN,与AB相对的下底面的面对角线平行,且与直线NQ垂直,可得AB垂直于平面MNQ;
对于C,AB为前面的面对角线,显然AB垂直于MN,QN在下底面且与棱平行,此棱垂直于AB所在的面,即有AB垂直于QN,可得AB垂直于平面MNQ;
对于D,AB为上底面的对角线,MN平行于前面的一条对角线,此对角线与AB所成角为![]() ,
,
则AB不垂直于平面MNQ.
故选:D.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目