题目内容
设f(x)=4x2-1,g(x)=-2x+1(1)若关于x的方程f(2x)=2g(x)+m有负实数根,求m的取值范围;
(2)若F(x)=af(x)+bg(x)(a,b都为常数,且a>0)
①证明:当0≤x≤1时,F(x)的最大值是|2a-b|+a;
②求证:当0≤x≤1时,F(x)+|2a-b|+a≥0.
【答案】分析:(1)x<0,设2x=t,则t∈(0,1), ,问题转化为求4
,问题转化为求4 -1值域,由此可解;
-1值域,由此可解;
(2)F(x)=4ax2-2bx+b-a的对称轴 ,①分两种情况讨论:当
,①分两种情况讨论:当 时,当
时,当 时,;
时,;
②即求证F(x)min+|2a-b|+a≥0,按 、
、 、
、 三种情况讨论求出F(x)min即可;
三种情况讨论求出F(x)min即可;
解答:解:(1)当x<0时,设2x=t,则t∈(0,1), ,
,
∵ ,∴m<1.
,∴m<1.
故m的取值范围为(-∞,1).
(2)证明:F(x)=4ax2-2bx+b-a,对称轴 ,
,
①当 即2a≥b时,F(x)max=F(1)=3a-b,
即2a≥b时,F(x)max=F(1)=3a-b,
当 即2a<b时,F(x)max=F(0)=b-a,
即2a<b时,F(x)max=F(0)=b-a,
故 ;
;
②即求证F(x)min+|2a-b|+a≥0, ,
,
当 即b≤0时,F(x)min+|2a-b|+a=F(0)+2a-b+a=2a>0,
即b≤0时,F(x)min+|2a-b|+a=F(0)+2a-b+a=2a>0,
当 即0<b<4a时,F(x)min+|2a-b|+a=F(
即0<b<4a时,F(x)min+|2a-b|+a=F(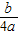 )+|2a-b|+a=
)+|2a-b|+a= ,
,
∴F(x)min+|2a-b|+a>0,
当 即b≥4a时,F(x)min+|2a-b|+a=F(1)+b-a=2a>0,
即b≥4a时,F(x)min+|2a-b|+a=F(1)+b-a=2a>0,
综上,当0≤x≤1时,F(x)+|2a-b|+a≥0.
点评:本题考查函数恒成立问题及二次函数最值问题,考查分类讨论思想,考查学生分析问题解决问题的能力.
 ,问题转化为求4
,问题转化为求4 -1值域,由此可解;
-1值域,由此可解;(2)F(x)=4ax2-2bx+b-a的对称轴
 ,①分两种情况讨论:当
,①分两种情况讨论:当 时,当
时,当 时,;
时,;②即求证F(x)min+|2a-b|+a≥0,按
 、
、 、
、 三种情况讨论求出F(x)min即可;
三种情况讨论求出F(x)min即可;解答:解:(1)当x<0时,设2x=t,则t∈(0,1),
 ,
,∵
 ,∴m<1.
,∴m<1.故m的取值范围为(-∞,1).
(2)证明:F(x)=4ax2-2bx+b-a,对称轴
 ,
,①当
 即2a≥b时,F(x)max=F(1)=3a-b,
即2a≥b时,F(x)max=F(1)=3a-b,当
 即2a<b时,F(x)max=F(0)=b-a,
即2a<b时,F(x)max=F(0)=b-a,故
 ;
;②即求证F(x)min+|2a-b|+a≥0,
 ,
,当
 即b≤0时,F(x)min+|2a-b|+a=F(0)+2a-b+a=2a>0,
即b≤0时,F(x)min+|2a-b|+a=F(0)+2a-b+a=2a>0,当
 即0<b<4a时,F(x)min+|2a-b|+a=F(
即0<b<4a时,F(x)min+|2a-b|+a=F(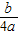 )+|2a-b|+a=
)+|2a-b|+a= ,
,∴F(x)min+|2a-b|+a>0,
当
 即b≥4a时,F(x)min+|2a-b|+a=F(1)+b-a=2a>0,
即b≥4a时,F(x)min+|2a-b|+a=F(1)+b-a=2a>0,综上,当0≤x≤1时,F(x)+|2a-b|+a≥0.
点评:本题考查函数恒成立问题及二次函数最值问题,考查分类讨论思想,考查学生分析问题解决问题的能力.

练习册系列答案
相关题目