题目内容
4．在△ABC中，内角A，B，C所对的边分别是a，b，c，已知C=$\frac{π}{3}$若a=2，b=3，求△ABC的外接圆的面积．分析 由已知及余弦定理可求c的值，由正弦定理得外接圆半径R的值，从而可求△ABC的外接圆的面积S=4πR2．
解答 解：∵C=$\frac{π}{3}$若a=2，b=3，
∴由余弦定理得：c2=a2+b2-2abcosC=7，可解得：c=$\sqrt{7}$，
由正弦定理得：$\frac{c}{sinC}=2R$=$\frac{\sqrt{7}}{\frac{\sqrt{3}}{2}}$，
解得：R=$\frac{\sqrt{21}}{3}$，
∴△ABC的外接圆的面积：S=4πR2=$\frac{28π}{3}$．
点评 本题主要考查了正弦定理，余弦定理的综合应用，属于基本知识的考查．
练习册系列答案
相关题目
16．若某校研究性学习小组共6人，计划同时参观科普展，该科普展共有甲，乙，丙三个展厅，6人各自随机地确定参观顺序，在每个展厅参观一小时后去其他展厅，所有展厅参观结束后集合返回，设事件A为：在参观的第一小时时间内，甲，乙，丙三个展厅恰好分别有该小组的2个人；事件B为：在参观的第二个小时时间内，该小组在甲展厅人数恰好为2人．则P（B|A）=（ ）
| A． | $\frac{3}{8}$ | B． | $\frac{1}{8}$ | C． | $\frac{3}{16}$ | D． | $\frac{1}{16}$ |
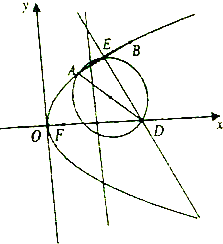已知F（1，0）是抛物线y2=2px（p＞0）的焦点．