题目内容
已知椭圆
+y2=1（a＞1）的两个焦点为F1、F2，P为椭圆上一点，且∠F1PF2=60°，则|PF1|•|PF2|的值为（ ）A．1
B．
C．
D．
【答案】分析：先设出|PF1|=m，|PF2|=n，利用椭圆的定义求得n+m的值，平方后求得mn和m2+n2的关系，代入△F1PF2的余弦定理中求得mn的值．
解答：解：设|PF1|=m，|PF2|=n，
由椭圆的定义可知m+n=2a，
∴m2+n2+2nm=4a2，
∴m2+n2=4a2-2nm
由余弦定理可知cos60°=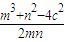
=
=
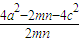，求得mn=
故选C．
点评：本题主要考查了椭圆的应用，椭圆的简单性质和椭圆的定义．考查了考生对所学知识的综合运用．
解答：解：设|PF1|=m，|PF2|=n，
由椭圆的定义可知m+n=2a，
∴m2+n2+2nm=4a2，
∴m2+n2=4a2-2nm
由余弦定理可知cos60°=
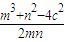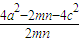==，求得mn=故选C．
点评：本题主要考查了椭圆的应用，椭圆的简单性质和椭圆的定义．考查了考生对所学知识的综合运用．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
+y2=1(a≥2),直线l与椭圆交于A,B两点,M是线段AB的中点,连结OM并延长交椭圆于点C.
,求椭圆的离心率;
+y2=1的左、右焦点为F1、F2，上顶点为A，直线AF1交椭圆于B．如图所示沿x轴折起，使得平面AF1F2⊥平面BF1F2．点O为坐标原点．
+y2=1上一点M到点（1，0）的距离是
，则点M到直线x=-2的距离是（ ）
+y2=1（a＞1）的两个焦点为F1、F2，P为椭圆上一点，且∠F1PF2=60°，则|PF1|•|PF2|的值为（ ）
