题目内容
已知函数f(x)=ln(ex+a)(a为常数,e=2.71828…)是R上的奇函数.
(Ⅰ)求a的值;
(Ⅱ)讨论关于x的方程 的根的个.
的根的个.
解:(Ⅰ)由f(x)=ln(ex+a)是R的奇函数,则f(-x)=-f(x),
不妨去x=0,可得f(0)=ln(e0+a)=0,解得a=0.…..…..(4分)
(Ⅱ)由(Ⅰ)可得f(x)=lnex=x,故 ,
,
令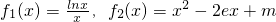 ,则
,则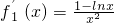 ,
,
当x∈(0,e)时,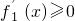 ,∴f1(x)在(0,e]上为增函数;
,∴f1(x)在(0,e]上为增函数;
当x∈[e,+∞)时,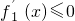 ,∴f1(x)在[e,+∞)上为减函数;
,∴f1(x)在[e,+∞)上为减函数;
当x=e时,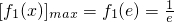 ,….…..(8分)
,….…..(8分)
而 ,结合函数图象可知:
,结合函数图象可知:
当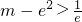 ,即
,即 时,方程无解;
时,方程无解;
当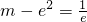 ,即
,即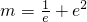 时,方程有一个根x=e;
时,方程有一个根x=e;
当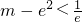 ,即
,即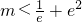 时,方程有两个根.…..…..….(12分)
时,方程有两个根.…..…..….(12分)
分析:(Ⅰ)由奇函数的性质可得f(-x)=-f(x),令x=0代入可得a值;
(Ⅱ)代入可得 ,令
,令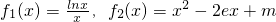 ,求导数可得函数f1(x)的单调性,进而得最大值,配方可得
,求导数可得函数f1(x)的单调性,进而得最大值,配方可得 ,结合函数图象可知得结论.
,结合函数图象可知得结论.
点评:本题考查函数的奇偶性和根的存在性及个数的判断,属中档题.
不妨去x=0,可得f(0)=ln(e0+a)=0,解得a=0.…..…..(4分)
(Ⅱ)由(Ⅰ)可得f(x)=lnex=x,故
 ,
,令
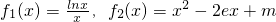 ,则
,则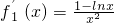 ,
,当x∈(0,e)时,
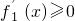 ,∴f1(x)在(0,e]上为增函数;
,∴f1(x)在(0,e]上为增函数;当x∈[e,+∞)时,
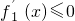 ,∴f1(x)在[e,+∞)上为减函数;
,∴f1(x)在[e,+∞)上为减函数;当x=e时,
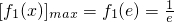 ,….…..(8分)
,….…..(8分)而
 ,结合函数图象可知:
,结合函数图象可知:当
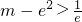 ,即
,即 时,方程无解;
时,方程无解;当
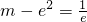 ,即
,即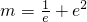 时,方程有一个根x=e;
时,方程有一个根x=e;当
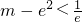 ,即
,即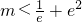 时,方程有两个根.…..…..….(12分)
时,方程有两个根.…..…..….(12分)分析:(Ⅰ)由奇函数的性质可得f(-x)=-f(x),令x=0代入可得a值;
(Ⅱ)代入可得
 ,令
,令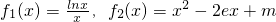 ,求导数可得函数f1(x)的单调性,进而得最大值,配方可得
,求导数可得函数f1(x)的单调性,进而得最大值,配方可得 ,结合函数图象可知得结论.
,结合函数图象可知得结论.点评:本题考查函数的奇偶性和根的存在性及个数的判断,属中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目